Задача 2 Транспортная задача.. Задача 3. Решить методом неопределенных множителей Лагранжа

Задача 2 Транспортная задача.

В регионе имеется 5 источников товара и 15 потребителей. Запасы источников, спрос потребителей и матрица транспортных затрат (по вариантам) приведены ниже.

Заданиеэ

1. Сформировать оптимальный план перевозок (по вариантам)

2. Описать процесс и результаты решения задачи, оформить отчет.

Решение выполнять инструментом "Поиск решения" программы MS Excel

Запасы источников
Пункт	Объем

Спрос потребителей
Пункт	Объем

Матрица транспортных затрат

Источник

Потребители

Вар. 1

Вар. 2

Вар. 3

Вар. 4

Вар. 5

Вар. 6

Вар. 7

Вар. 8

Источник

Потребители

Вар. 9

Вар. 10

Вар. 11

Вар. 12

Вар. 13

Вар. 14

Вар. 15

Вар. 16

Источник

Потребители

Вар. 17

Вар. 18

Вар. 19

Вар. 20

Задача 3. Решить методом неопределенных множителей Лагранжа

Задание. Предприятие производит продукцию 2-мя различными технологическими способами. Функции производственных затрат 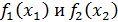имеют вид:

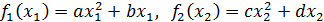, где 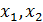– объемы производства продукции 1-м и 2-м способами.

Задание.

1. Определить сколько изделий каждым из способов необходимо изготовить, чтобы общие затраты на производство были минимальные, если по плану производства предприятию необходимо изготовить V единиц продукции.

2. Оформить решение.

Требование: задача решается аналитически, без привлечения программных средств и онлайн-сервисов.

вариант	a	b	c	d	V
	0,11			0,05
	0,21			0,06
	0,24			0,06
	0,19			0,05
	0,15			0,11
	0,22			0,12
	0,18			0,19
	0,22			0,14
	0,17			0,14
	0,14			0,18
	0,19			0,11
	0,13			0,14
	0,22			0,15
	0,18			0,16
	0,3			0,19
	0,25			0,07
	0,13			0,08
	0,11			0,06
	0,19			0,16
	0,24			0,07

Задача 4

Небольшой магазин с одним продавцом. Входной поток покупателей пуассоновский с интенсивностью lчел./час, интенсивность обслуживания – m чел./час, время обслуживания распределено экспоненциально. Максимальная длина очереди к продавцу – m человек После введения ограничений, связанных с пандемией, интенсивность потока покупателей снизилась до величины kl, k<1.

Задание.

1. Определить, на сколько в среднем снизилась выручка магазина, если средняя сумма покупки одним покупателем 500 р.

2. Оформить решение.

Рекомендация: найти вероятность обслуживания и абсолютную пропускную способность до и после введения ограничений.

Вариант	l чел./час	m чел./час	m чел.	k
	40,9	51,7		0,15
	51,6	61,6		0,09
	58,7			0,1
	53,8	68,4		0,04
	53,5	68,4		0,13
	41,4	53,3		0,06
	42,7	52,1		0,18
	48,7	58,3		0,14
		57,7		0,11
	50,9	60,5		0,15
	49,4	56,9		0,05
	46,9	60,8		0,01
	54,1	61,1		0,23
	41,6	54,2		0,17
	40,9	51,4		0,29
	56,6	70,6		0,15
	67,5	76,6		0,26
	58,2			0,22
	51,8	62,3		0,21
	57,5	71,6		0,24

Задача 5. Управление запасами

Условия.

1) Склад однопродуктовый, одиночный

2) Спрос детерминированный, стационарный с интенсивностью m

3) Поставки мгновенные

4) Дефицит отсутствует

5) Затраты на заказ фиксированные, заказ делается когда текущий запас на складе равен 0

6) Затраты пропорциональны ср. запасу

m – интенсивность спроса

Y – величина поставки

a – затраты на хранение единицы товара в ед. времени

С – затраты на заказ

z0 – суммарные затраты

z1 – затраты на хранение товара в ед. времени

z2 – затраты на заказ в ед. времени

Т – интервал времени между поставками

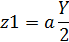
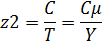
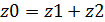
Задание.

1. Определить величину поставки, минимизирующую суммарные затраты z0 и интервал времени между поставками.

2. Оформить решение.

Рекомендация: Использовать формулы Уилсона

((__lxGc__=window.__lxGc__||{'s':{},'b':0})['s']['_228469']=__lxGc__['s']['_228469']||{'b':{}})['b']['_699880']={'i':__lxGc__.b++};

Вариант	m	a	C

⇐ Предыдущая 12