
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задания из первой части по алгебре.
Задания из первой части по алгебре.

1) определитесь с порядком действий:
1. возведение в степень (показатель степени указывает сколько раз число умножается само на себя)
2. умножение
3. сложение (вычитание)
2) при умножении не забывайте пользоваться правилом умножения положительных и отрицательных чисел:
1. "+"*"+"="+"
2. "-"*"-"="+"
3. "+"*"-"="-"
Тогда получаем следующее решение:


В этот раз задание 7 оказалось самым простым из всех возможных.
Достаточно понимать, что число можно представить в виде корня из числа в квадрате. Значит крайние числа промежутка необходимо представить в виде "корней". Т.е. 7 это корень из 49, а 8 это корень из 64.
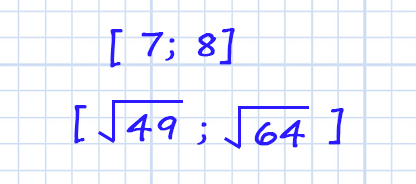
Теперь видно, что единственное число, которое окажется между крайними числами промежутка, находится под 4 вариантом ответов.


Задание на свойства степеней.
Для решения воспользуемся свойством умножения степеней с одинаковым основанием и определением отрицательной степени.
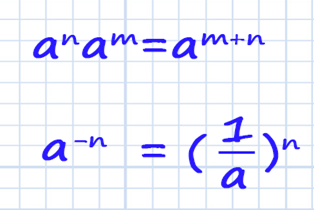
Выполняем умножение дробей: числитель умножаем на числитель, знаменатель на знаменатель. В знаменателе получаем умножение степеней с основанием 4. Степени складываем основанием переписываем.
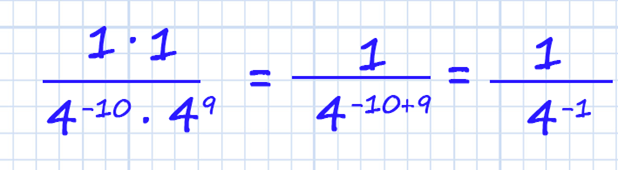
Отрицательная степень это та же положительная степень, только обратного числа. Находим число обратное 4 (это 1/4). И чтобы не строить трехэтажную дробь, записываем через знак деления:
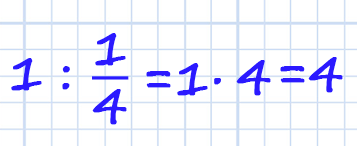


Все что содержит "х" находится слева от "равно". Число находится справа. Остается только упростить левую часть уравнения.
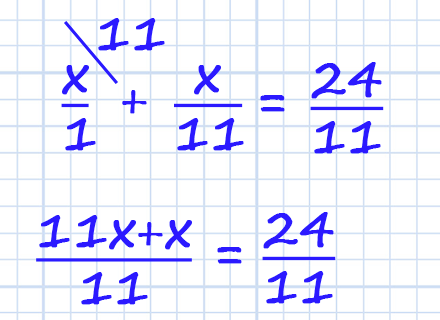
И слева, и справа в равенстве дробные выражения с одинаковым знаменателем. Дроби равны, знаменатели равны, следовательно числители равны.

Осталось найти "х" как неизвестный множитель и записать ответ.

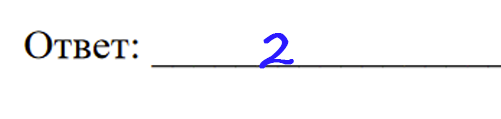

Задание на классическое определение вероятности.

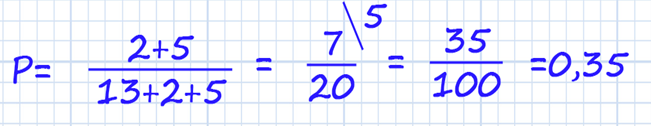

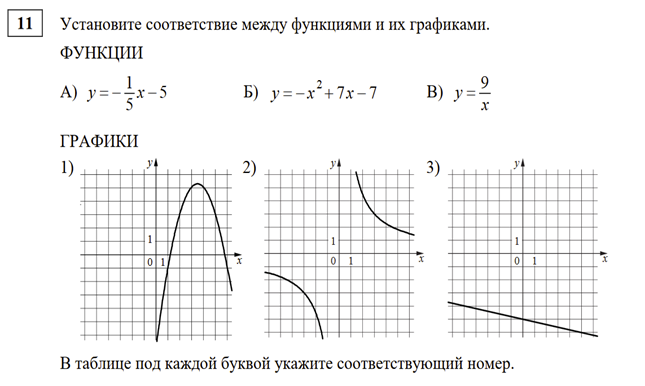

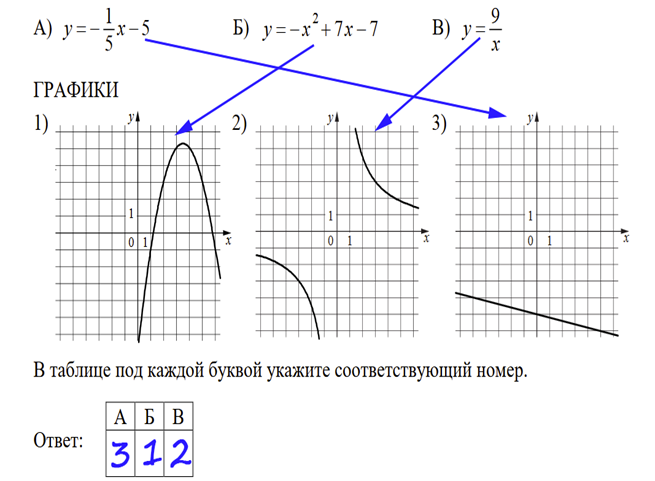
Конкретно в этом задании достаточно понимать как выглядят графики функций в общем виде:
И исходя из этого сопоставим функции и их графики:

В этих заданиях можно выразить неизвестную и потом подставить числовые значения, а лучше сразу подставить числовые значения и потом находить неизвестную.
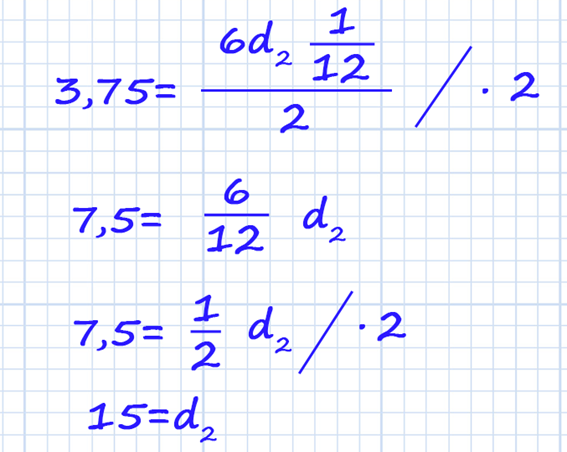

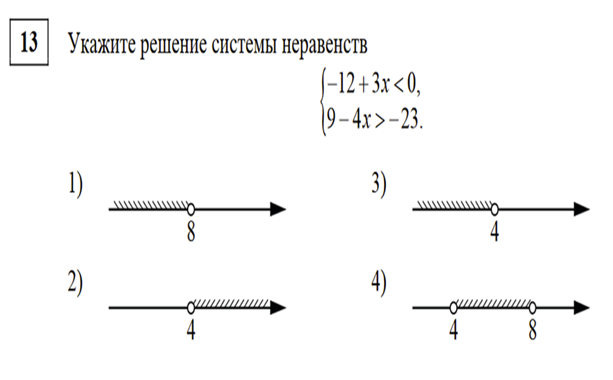
Решаем два линейных неравенства:
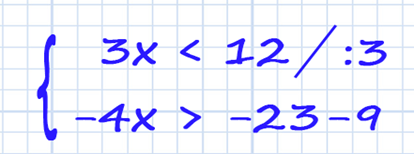
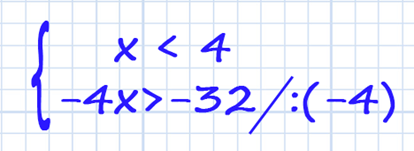
не забывайте, при делении на отрицательное число знак неравенства переворачивается!
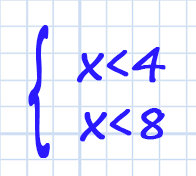
На числовой прямой закрашиваем сначала решение первого неравенства:

Затем на этой же числовой прямой закрашиваем интервал второго неравенства:
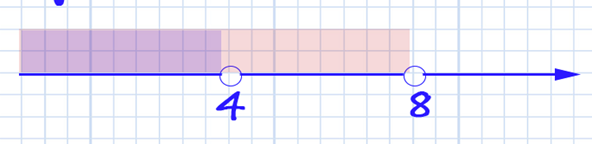
Решением считается пересечение интервалов (там, где интервалы закрашены одновременно).
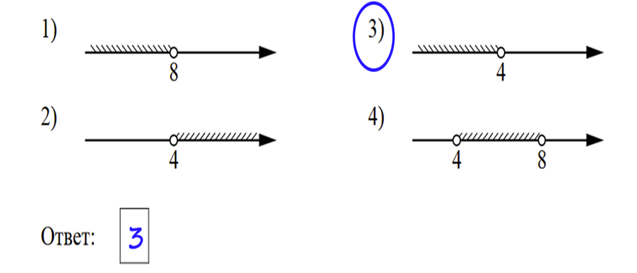

Как решать такие задания и откуда формулы разбирали здесь, так что если вы ничего не знаете про арифметическую прогрессию загляните сначала туда :)
Воспользуемся для решения задачи формулами из справочных материалов:

Запишем, что дано по условию:
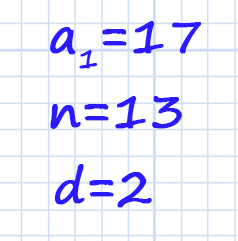
Рассчитаем количество мест в последнем (13-ом) ряду:

А теперь по формуле легко найдем количество всех мест в театре, как сумму арифметической прогрессии.
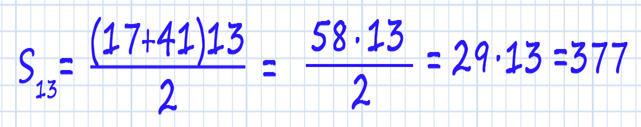

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|