
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ОБРАЗЦЫ ВЫПОЛНЕНИЯ ЗАДАНИЙ
ОБРАЗЦЫ ВЫПОЛНЕНИЯ ЗАДАНИЙ
Задача 1. Коллинеарны ли векторы 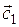 и
и 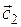 , построенные по векторам
, построенные по векторам 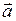 и
и 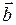 ?
?
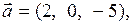
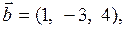
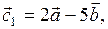
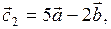
Решение: Найдём координаты векторов 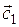 и
и 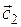 .
.
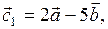 ,
,
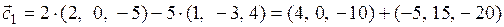 ,
,
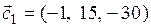 ,
,
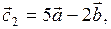 ,
,
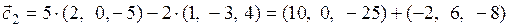 ,
,
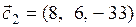 .
.
Векторы  и
и 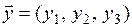 коллинеарны, если их координаты пропорциональны, то есть
коллинеарны, если их координаты пропорциональны, то есть
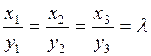 .
.
Так как
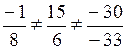 ,
,
то векторы 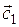 и
и 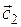 не являются коллинеарными.
не являются коллинеарными.
Ответ: векторы 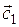 и
и 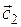 не являются коллинеарными.
не являются коллинеарными.
Задача 2. Найти косинус угла между векторами  и
и 

Решение: Найдём координаты векторов  и
и  :
:
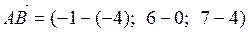 ,
,
 ,
,
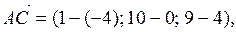
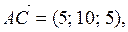
Косинус угла между векторами  и
и 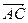 находится по формуле:
находится по формуле:
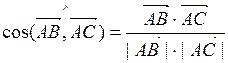 ,
,
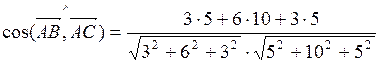 ,
,
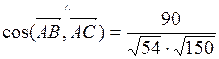 ,
,
 ,
,
тогда 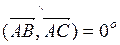 .
.
Задача 3.Компланарны ли векторы 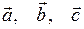 ?
?
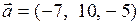 ,
, 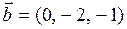 ,
, 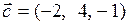
Решение. Векторы 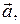
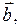
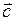 компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
Найдём смешанное произведение векторов 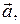
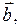
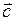 по формуле:
по формуле:
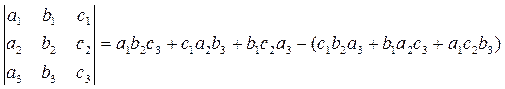
При этом полезна следующая схема. Первые три слагаемых – это произведения элементов, попавших на главную диагональ и в вершины двух треугольников (рис.1). Три слагаемых в скобках – это произведения элементов, попавших на побочную диагональ и в вершины двух других треугольников (рис.2).
 | |||
 | |||
Рис. 1 Рис. 2
Получаем
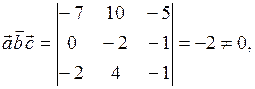
следовательно, векторы 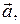
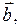
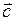 некомпланарны, то есть не лежат в одной плоскости.
некомпланарны, то есть не лежат в одной плоскости.
Ответ: векторы 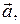
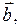
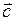 некомпланарны.
некомпланарны.
Задача 4. Даны вершины тетраэдра 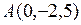 ,
, 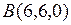 ,
, 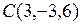 ,
,  . Найти объём.
. Найти объём.
Решение.
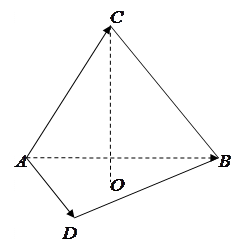
Так как тетраэдр  построен на векторах
построен на векторах  ,
, 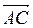 ,
,  , то его объём равен
, то его объём равен
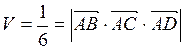 .
.
Найдём координаты векторов  ,
, 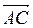 ,
,  .
.
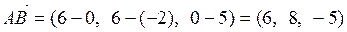 ,
,
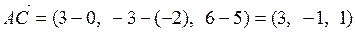 ,
,
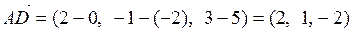 .
.
Тогда
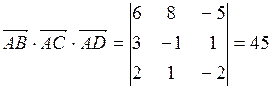 .
.
 (куб. ед.).
(куб. ед.).
Ответ:  (куб. ед.).
(куб. ед.).
Решить самостоятельно!!!!!!!!!!
Задача 1. Коллинеарны ли векторы 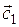 и и 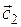 , построенные по векторам , построенные по векторам 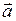 и и 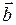 ? ?
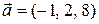 , , 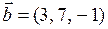 , , 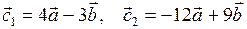 .
Задача 2. Найти косинус угла между векторами .
Задача 2. Найти косинус угла между векторами 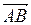 и и 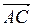 . .
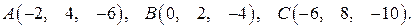 Задача 3. Компланарны ли векторы
Задача 3. Компланарны ли векторы 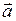 , , 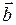 и и 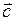 ? ?
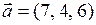 , , 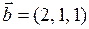 , , 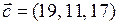 . .
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|