Вариант от 11.01.21( решить к 16.01) Часть 1.

Вариант от 11.01.21( решить к 16.01) Часть 1.

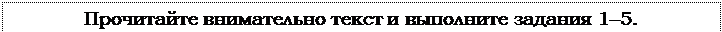
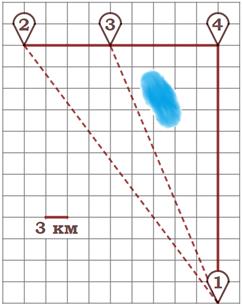Дима летом отдыхает у дедушки в деревне Ва- сильевка. Во вторник они собираются съездить на велосипедах в село Плодородное на ярмарку. Из деревни Васильевка в село Плодородное можно проехать по прямой лесной дорожке. Есть более длинный путь: по прямолинейному шоссе через деревню Шарковка до деревни Рас- свет, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в село Плодо- родное. Есть и третий маршрут: в деревне Шар- ковка можно свернуть на прямую тропинку в село Плодородное, которая идёт мимо пруда. Лесная дорожка и тропинка образуют с шоссе прямоугольные треугольники.

По шоссе Дима с дедушкой едут со скоростью 30 км/ч, а по лесной дорожке и тропинке – со скоростью 18 км/ч. На плане изображено взаимное распо- ложение населённых пунктов, длина стороны каждой клетки равна 3 км.

1. Пользуясь описанием, определите, какими цифрами на плане обозна- чены населённые пункты.

Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.

Насел. пункты	д. Рассвет	с. Плодородное	д. Васильевка
Цифры

Ответ: .

2. Сколько километров проедут Дима с дедушкой от деревни Васильевка до села Плодородное, если они поедут по шоссе через деревню Рассвет?

Ответ: .

3. Найдите расстояние от деревни Васильевка до села Плодородное по пря- мой. Ответ дайте в километрах.

Ответ: .

4. Сколько минут затратят на дорогу из деревни Васильевка в село Плодо- родное Дима с дедушкой, если они поедут сначала по шоссе, а затем свер- нут в Шарковке на прямую тропинку, которая проходит мимо пруда?

Ответ: .

5. В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Васильевка, селе Плодородное, де- ревне Шарковка и деревне Рассвет.

Наименование продукта	д. Васильевка	с. Плодородное	д. Шарковка	д. Рассвет
Молоко (1 л)
Хлеб (1 батон)
Сыр «Российский» (1 кг)
Говядина (1 кг)
Картофель (1 кг)

Дима с дедушкой хотят купить 2 л молока, 3 кг говядины и 2 кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.

Ответ: .

6.Найдите значение выражения 1,4 1- 4

Ответ: .

7. На координатной прямой отмечено число a. Какое из утверждений для этого числа является верным?

1) 4 -a > 0

2) a -7<0

3) a - 8 > 0

4) 8 -a < 0

Ответ: .

8. Найдите значение выражения

49 +( 4,9)² .

Ответ: .

9.Найдите корень уравнения -3x +1- 3(x +3)= -2(1- x )+2 .

Ответ: .

10. В лыжных гонках участвуют 12 спортсменов из России, 5 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из России.

Ответ: .

11. На рисунке изображены графики функций вида y = ax ² +bx+ c . Уста-

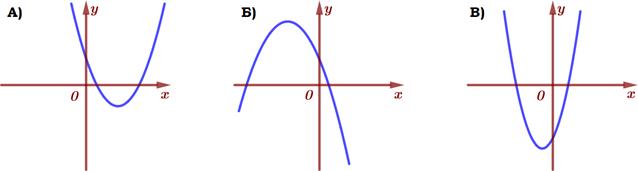новите соответствие между графиками функций и знаками коэффициен- тов.

1) a <0, c<0 2) a >0, c<0 3) a >0, c>0 4) a <0, c>0

Ответ:

В таблице под каждой буквой укажите соответствую- щий номер.

12. Чтобы перевести значение температуры по шкале Цельсия в шкалу

Фаренгейта, пользуются формулой

tF =1,8tC +32 , где tC

– градусы Цельсия,

tF – градусы Фаренгейта. Скольким градусам по шкале Фаренгейта соот-

ветствует –56 градусов по шкале Цельсия?

Ответ: .

13. Укажите решение неравенства 25x² ³ 64 .

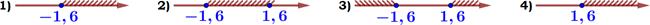Ответ: .

14. В течение 25 банковских дней акции компании дорожали ежедневно на одну и ту же сумму. Сколько стоила акция компании в последний день этого периода, если в 7–й день акция стоила 821 рублей, а в 16–й день – 974 рублей.

Ответ: .

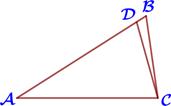
15.Точка D на стороне AB треугольника ABC выбрана так, что AD = AC . Известно, что ÐCAB= 32° и ÐACB= 82°. Найдите ÐDCB . От- вет дайте в градусах. Ответ: .

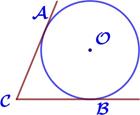
16.В угол C величиной 67° вписана окруж- ность, которая касается сторон угла в точках A и B, точка O – центр окружности. Найдите угол AOB. Ответ дайте в градусах. Ответ: .

17.В равнобедренной трапеции основания равны 5 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции. Ответ: .

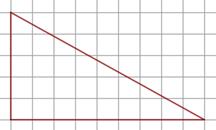
18.На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник. Найдите длину его большего катета. Ответ: .

19. Какие из следующих утверждений верны?

1) Если две стороны одного треугольника соответственно равны двум сто- ронам другого треугольника, то такие треугольники равны.

2) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

3) Любые два равносторонних треугольника подобны.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

20. Решите уравнение

Часть 2.

(x ² - 81)² +(x ² +5x - 36)² = 0 .

Ответ: .

21. Дорога между пунктами A и В состоит из подъёма и спуска, а её длина равна 13 км. Турист прошёл путь из А в В за 5 часов, из которых спуск занял 3 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 1 км/ч?

22. Постройте график функции

y= x² +3x - 3 x +2 +2

и определите, при ка-

ких значениях m прямая y = m имеет с графиком ровно три общие точки.

23. Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке

K. Найдите площадь параллелограмма, если BC =14 , а расстояние от точки K до стороны AB равно 5.

24. В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O. Докажите, что площади треугольников AOB и COD равны.

25. В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 28. Найдите стороны треугольника ABC.