ВАРИАНТ 6 Вариант № 34184537. Задание 1 № 26637. Задание 2 № 501738. Задание 3 № 245007. Задание 4 № 320189. Задание 5 № 26661. Задание 6 № 27828. Задание 7 № 27500

ВАРИАНТ 6 Вариант № 34184537

Задание 1 № 26637

На день рождения полагается дарить букет из нечетного числа цветов. Тюльпаны стоят 30 рублей за штуку. У Вани есть 500 рублей. Из какого наибольшего числа тюльпанов он может купить букет Маше на день рождения?

Задание 2 № 501738

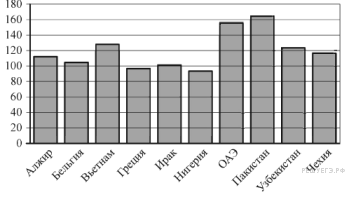
На диаграмме показано распределение выбросов углекислого газа в атмосферу в 10 странах мира (в миллионах тонн) за 2008 год. Среди представленных стран первое место по объёму выбросов занимал Пакистан, десятое место — Нигерия. Какое место среди представленных стран занимала Чехия?

Задание 3 № 245007

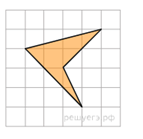
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 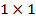см (см. рис.). Ответ дайте в квадратных сантиметрах.

Задание 4 № 320189

В некотором городе из 5000 появившихся на свет младенцев 2512 мальчиков. Найдите частоту рождения девочек в этом городе. Результат округлите до тысячных.

Задание 5 № 26661

Найдите корень уравнения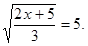

Задание 6 № 27828

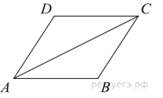
Найдите большую диагональ ромба, сторона которого равна 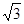, а острый угол равен 60°.

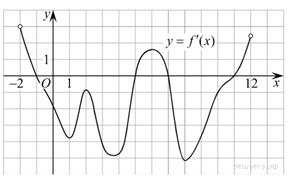
Задание 7 № 27500

На рисунке изображен график производной функции f(x), определенной на интервале (−2; 12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.

Задание 8 № 245345

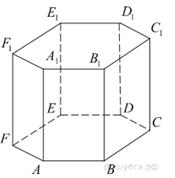
Найдите объем многогранника, вершинами которого являются точки A, B, D, E, A₁, B₁, D₁, E₁, правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 6, а боковое ребро равно 2.

Задание 9 № 26776

Найдите 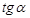, если 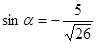и

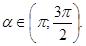
Задание 10 № 319859

Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности In, оперативности Op, объективности публикаций Tr, а также качества сайта Q. Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от 1 до 5.

Аналитики, составляющие формулу рейтинга, считают, что объективность ценится втрое, а информативность публикаций — вдвое дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид

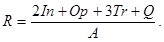
Каким должно быть число A, чтобы издание, у которого все оценки наибольшие, получило бы рейтинг 1?

Задание 11 № 99588

Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч?

Задание 12 № 77468

Найдите точку минимума функции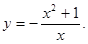

Задание 13 № 507595

а) Решите уравнение .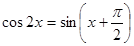

б) Найдите корни этого уравнения, принадлежащие промежутку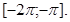

Задание 14 № 513684

В правильной четырехугольной призме ABCDA₁B₁C₁D₁ точка K делит боковое ребро AA₁ в отношении AK : KA₁ = 1 : 2. Через точки B и K проведена плоскость α, параллельная прямой AC и пересекающая ребро DD₁ в точке M.

а) Докажите, что плоскость α делит ребро DD₁ в отношении DM : MD₁ = 2 : 1.

б) Найдите площадь сечения, если известно, что AB = 4, AA₁ = 6.

Задание 15 № 484584

Решите неравенство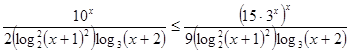

Задание 16 № 512338

Дана равнобедренная трапеция KLMN с основаниями KN и LM. Окружность с центром O, построенная на боковой стороне KL как на диаметре, касается боковой стороны MN и второй раз пересекает большее основание KN в точке H, точка Q — середина MN.

а) Докажите, что четырёхугольник NQOH — параллелограмм.

б) Найдите KN, если ∠LKN = 75° и LM = 1.

Задание 17 № 511255

Миша и Маша положили в один и тот же банк одинаковые суммы под 10% годовых. Через год сразу после начисления процентов Миша снял со своего счета 5000 рублей, а еще через год снова внес 5000 рублей. Маша, наоборот, через год доложила на свой счет 5000 рублей, а еще через год сразу после начисления процентов сняла со счета 5000 рублей. Кто через три года со времени первоначального вложения получит большую сумму и на сколько рублей?

Задание 18 № 513610

Найдите все значения a, при каждом из которых система уравнений

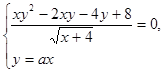
имеет ровно два различных решения.

Задание 19 № 525144

Вася и Петя решали задачи из сборника, причем каждый следующий день Вася решал на одну задачу больше, чем в предыдущий, а Петя — на две задачи больше, чем в предыдущий. В первый день каждый решил хотя бы одну задачу, а в итоге каждый решил все задачи сборника.

а) Могло ли быть в сборнике 85 задач?

б) Могло ли быть в сборнике 213 задач, если каждый из мальчиков решал их более трех дней?

в) Какое наибольшее количество дней мог решать задачи Петя, если Вася решил весь сборник за 16 дней, а количество задач в сборнике меньше 300.