Контрольная работа

Министерство образования и науки Российской Федерации

ФГАОУ ВО «УрФУ имени первого Президента России Б.Н. Ельцина»

Институт новых материалов и технологий

Кафедра «Металлургия железа и сплавов»

Оценка работы______________

Руководитель от УрФУ_________/Спирин Н.А.

Контрольная работа

1. На тему: «Точечные оценки основных параметров нормального закона распределения»

Студент Соловьев И.Д.

^{Подпись ФИО}

Группа НМТЗМ-102203

Екатеринбург 2021

Основными параметрами нормального закона распределения являются математическое ожидание и дисперсия.

Математическое ожидание – это сумма произведения дискретной случайной величины (X_i) с её вероятностью (p_i). Для начала зададим закон распределения для дискретной величины. Возьмем пример с погодой, например, сколько раз пойдет дождь за месяц. У каждой величины своя вероятность.

X_i
p_i	0,2	0,1	0,4	0,3

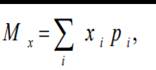Математическое ожидание будет рассчитываться по следующей формуле:

M_x = 4*0,2 + 5*0,1 + 2*0,4 + 3*0,3 = 3

Посчитав математическое ожидание, можно сказать, что в среднем за месяц три раза пройдёт дождь. То есть, математическое ожидание показывает средневзвешенную величину всех возможных значений, которые может принимать эта величина с какой-то долей вероятности.

Дисперсия случайной величины – это параметр, который показывает отклонение от математического ожидания случайной величины. Находится дисперсия по следующей формуле:

D(x) = M(x²) - (M_x)²

M(x²) – математическое ожидание случайной величины, которую возвели в квадрат; (M_x)² – математическое ожидание возведенное в квадрат

Для начала найдем M(x²):

M(x²) = 16*0,2+25*0,1+4*0,4+9*0,3 = 10

Вставляем полученное значение в формула для дисперсии:

D(x) = 10 – 9 = 1

Отклонение от количества в среднем выпадения дождя равно 1, т.е. за этот месяц возможно выпадет 2 или 4 раза дождь.

Подведем итог, при нормальной законе распределения случайной величины, можно вычислить два основных параметра – это математическое ожидание и дисперсия. Математическое ожидание – это средневзвешенная величина всех значений с долей вероятности, которая эта величина может принимать. Дисперсия – это параметр, который показывает отклонение от математического ожидания.