
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Определитель матрицы. Определитель матрицы – это ЧИСЛО, полученное по определенным правилам в зависимости от порядка матрицы. Определитель существует только для квадратных матриц!. Свойства определителей.
Определитель матрицы
Определитель матрицы – это ЧИСЛО, полученное по определенным правилам в зависимости от порядка матрицы. Определитель существует только для квадратных матриц!
· Определитель квадратной матрицы.
Определитель первого порядка представляет собой число.
Определитель квадратной матрицы порядка n A=(aij)m×n обозначается символами: 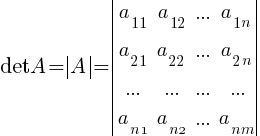
Определитель квадратной матрицы A второго порядка — это число, равное: 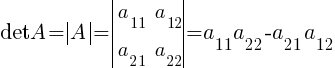
Определитель квадратной матрицы А третьего порядка — это число, равное:
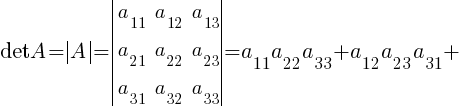
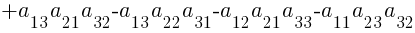 . Пример 7.
. Пример 7.
· Правило треугольников (правило Саррюса):
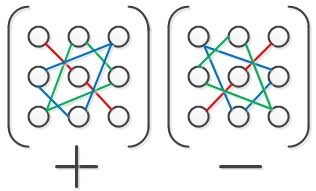
Знаки (+) и (–) соответствуют знакам определенных слагаемых, входящих в определитель, элементы определителя изображаются кружками, а соответствующие произведения — отрезками или треугольниками.
· Алгебраическое дополнение A=(aij) элемента aij — это определитель n-1 порядка, полученный из |A| вычеркиванием i-й строки и j-го столбца, на пересечении которых стоит элемент aij, взятый со знаком (-1)i+j.
Свойства определителей.
1. Определитель квадратной матрицы А не меняется при транспонировании: |AT|=|A|.
2. При перестановке местами любых двух строк (столбцов) определитель |A| меняет знак:
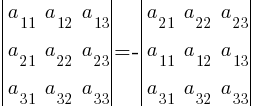
3. Определитель, содержащий две одинаковые строки (столбца), равен нулю.
4. Умножение всех элементов некоторой строки (столбца) определителя |A| на число k равносильно умножению определителя на это число:
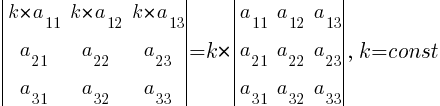
5. Если все элементы некоторой строки (столбца) определителя |A| равны нулю, то и сам определитель равен нулю (вытекает из предыдущего свойства при (k = 0):
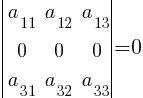
6. Если все элементы двух строк (столбцов) определителя |A| пропорциональны, то определитель равен нулю.
7. Если каждый элемент некоторой строки (столбца) определителя представляет собой сумму двух слагаемых, то такой определитель можно представить в виде суммы двух определителей:
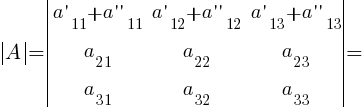
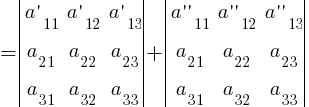
8. Если к элементам какой-нибудь строки (столбца) определителя |A| прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель k, то величина определителя не изменится:
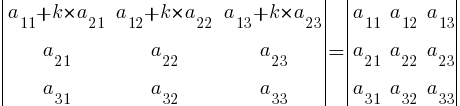
9. Определитель |A| численно равен сумме произведений элементов любой его строки (столбца) на соответствующие алгебраические дополнения:
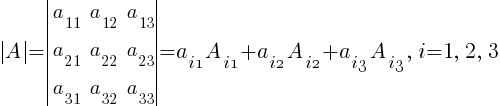
10. Определитель произведения матриц А и В равен произведению их определителей:
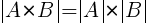 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|