Контакты

Случайная статья

п1.Свойства и графики тригонометрических функций.

Стр 1 из 2Следующая ⇒

п1.Свойства и графики тригонометрических функций.

Рассмотрим функцию .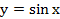

1. .

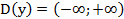2. .

3. Функция возрастает на 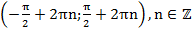и убывает на , .

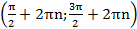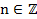4. Функция нечетна, то есть .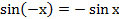

5. Функция периодична с периодом 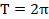, то есть .

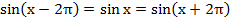6. Функция проходит через точки:


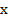
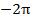
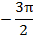
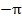
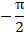
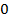
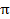
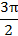
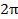
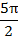
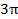
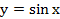
	0			-1				-1

Зам. При построении графиков тригонометрических функций удобно брать единицу масштаба равную 2 клеткам. Тогда, взяв 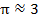, получим - 3 клетки, 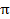- 6 клеток и т.д.

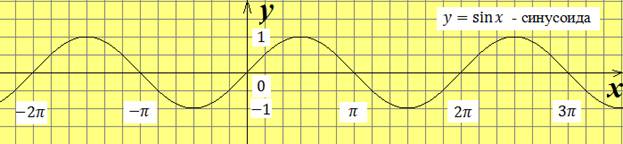
График функции 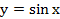называется синусоидой.

Рассмотрим функцию .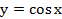

1. .

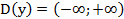2. .

3. Функция возрастает на 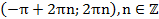и убывает на .

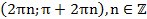4. Функция чётна, то есть .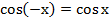

5. Функция периодична с периодом 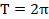, то есть .

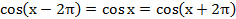6. Функция проходит через точки:


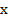
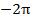
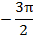
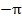
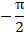
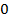
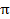
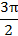
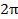
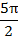
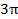
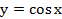
			-1				-1				-1

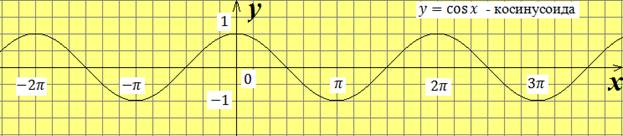
График функции 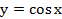называется косинусоидой.

Зам. Косинусоиду можно получить сдвигом синусоиды на влево. Данное преобразование отражено в формуле приведения: .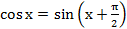

Рассмотрим функцию .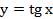

1. .

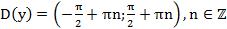2. .

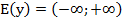3. Функция возрастает на .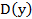

4. Функция нечётна, то есть .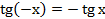

5. Функция периодична с периодом 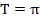, то есть .

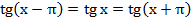6. График функции проходит через точки:

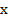
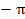
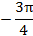
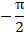
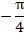
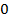
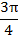
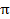
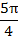
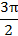
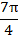
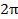
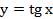
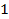
не сущ.

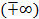
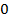
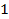
не сущ.

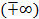
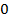
не сущ.

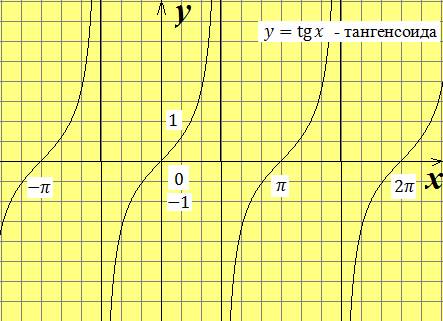
График функции 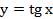называется тангенсоидой.

Рассмотрим функцию .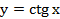

1. .

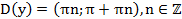2. .

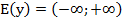3. Функция убывает на .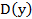

4. Функция нечётна, то есть .

5. Функция периодична с периодом 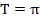, то есть .

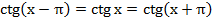6. График функции проходит через точки:

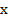
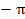
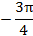
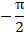
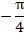
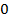
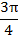
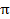
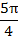
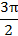
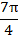
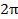
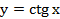
не сущ.

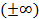
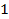
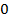
не сущ.

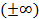
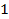
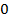
не сущ.

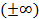
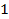
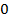
не сущ.

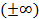
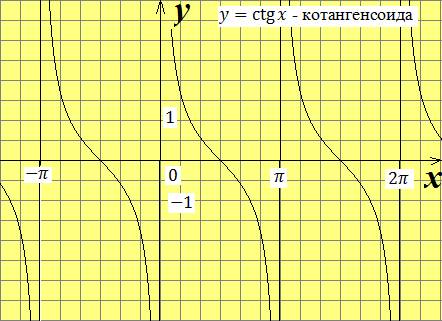
График функции 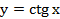называется котангенсоидой.

Зам. Котангенсоиду можно получить сдвигом тангенсоиды на влево и симметрией по оси 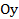. Данное преобразование отражено в формуле приведения: .

12 Следующая ⇒

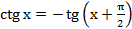© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.