Практическая работа № 1. Кульминация светил. Вид звездного неба на разных географических широтах

Практическая работа № 1

Кульминация светил. Вид звездного неба на разных географических широтах

Цель работы: изучение условий видимости небесных светил в различных местах земной поверхности.

Пособия: «Справочник любителя астрономии» П.Г. Куликовского; Малый звездный атлас А.А. Михайлова; калькулятор.

Видимое положение светил и любых точек на небесной сфере определяется двумя сферическими координатами. В астрономии используется несколько различных систем небесных координат. Выбор той или иной системы координат определяется содержанием выполняемой задачи. Однако, принцип построения всех систем сферических координат един.

На небесной сфере выбирается большой круг, принимаемый за основной круг системы координат. Именно он определяет название системы координат. Две диаметрально противоположные точки небесной сферы, удаленные на 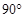от всех точек основного круга, называются полюсами этого круга.

Одна координата отсчитывается вдоль основного круга от некоторой выбранной точки, называемой нуль – пунктом системы координат. Вторая координата отсчитывается от основного круга в перпендикулярном направлении, вдоль большого круга, проходящего через полюса основного круга.

Рассмотрим наиболее часто используемые системы небесных координат.

Горизонтальная система координат. За основной круг принимается математический горизонт. Его полюсами являются точки зенита (Z) и надира (Na). Нуль-пунктом в горизонтальной системе координат является точка югаS на горизонте (рис. 1.1).

Положение небесного светила в горизонтальной системе определяется двумя координатами – азимутом А, изменяющимся в пределах от 0° до 360°, и высотой h, принимающей значения от 0° до ±90°.

АзимутА отсчитывается вдоль математического горизонта от точки юга S в западном направлении. Азимуты основных точек горизонта:

Рис. 1.1. Горизонтальная система координат

, , .

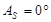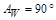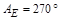Вторая координата – высота h – отсчитывается вдоль вертикального круга от математического горизонта до светила. Над горизонтом высота светила положительна, под горизонтом – отрицательна. Все точки горизонта имеют высоту 0°, зенит – 90°, надир – -90°.

В практике наблюдений часто измеряют не высоту h, а зенитное расстояние 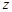, то есть, удаленность светила от точки зенита до светила вдоль вертикального круга. Очевидно, что связь между высотой и зенитным расстоянием определяется формулой:

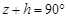(1.1)

Зенитное расстояние всегда положительно и изменяется в пределах от 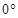(точка Z) до 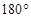(Na). Все точки, лежащие на одном альмукантарате, имеют одинаковую высоту и зенитное расстояние.

При суточном вращении небесной сферы горизонтальные координаты светил непрерывно изменяются, принимая в различные моменты времени строго определенные различные значения. Это позволяет заранее вычислять горизонтальные координаты небесных светил и определять условия их видимости в заданные моменты времени. Но для составления звездных карт, списков и каталогов небесных объектов горизонтальная система координат не пригодна. Для этой цели требуется такая система координат, в которой вращение небесной сферы не влияло бы на значения обеих координат светила.

Экваториальные системы координат. Для неизменности сферических координат необходимо, чтобы координатная сетка вращалась вместе с небесной сферой. Наиболее пригодны для этих целей экваториальные системы координат. В них за основной круг принимается небесный экватор, полюсами которого являются северный и южный полюсы мира.

Первая экваториальная система координат. За нуль-пункт в первой экваториальной системе принимается южная точка небесного экватора 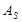, не изменяющая своего положения на небе относительно горизонта при суточном вращении неба. От этой точки вдоль небесного экватора в направлении суточного вращения небесной сферы отсчитывается координата, называемая часовым углом t (рис. 2.2). Часовые углы измеряются вчасовой мере и пределы их значений: от 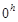до 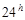.Вторая координата – склонениеd. Так называется дуга круга склонения от небесного экватора до светила. Склонение измеряется в градусной мере и изменяется в пределах: от 0⁰до 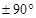. В северном полушарии неба склонение положительно, а в южном отрицательно.

Иногда вместо склонения используется так называемое полярное расстояние 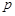, измеряемое дугой круга склонения от северного полюса мира 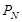до светила. Полярное расстояние всегда положительно и изменяется в пределах от 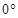(точка 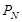) до 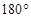( 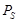). Полярное расстояние связано со склонением 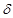светила следующим соотношением:

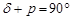(1.2)

Все точки небесной сферы, лежащие на одной небесной параллели, имеют одно и тоже склонение. При суточном вращении небесной сферы любое светило движется, описывая круг, вдоль небесной параллели, при этом его склонение не изменяется. Однако вторая координата – часовой угол светила – при суточном вращении неба непрерывно меняется. В связи с этим использовать первую экваториальную систему координат при составлении звездных карт и списков звезд нельзя.

Рис. 1.2. Экваториальные системы координат

Обычно первая экваториальная система координат используется в процессе астрономических наблюдений при наведении телескопа на светило.

Вторая экваториальная система небесных координат. В этой системе координат основной круг – небесный экватор, а нуль-пункт – точка весеннего равноденствия на нем. Она вместе со всеми точками небесного экватора участвует в суточном вращении небесной сферы.

Во второй экваториальной системе координат положение светила на небесной сфере также определяется двумя координатами (рис. 1.2). Одна из них – по-прежнему – склонение δ. Другая называется прямым восхождением и обозначается .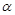

Прямым восхождением 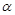называется дуга небесного экватора от точки весеннего равноденствия ^ до точки пересечения небесного экватора с кругом склонения светила. Прямое восхождение всегда положительно, отсчитывается в направлении против суточного вращения небесной сферы, то есть с запада на восток, измеряется во временных единицах и изменяетсяв пределах от 0^hдо 24^h.

Координаты светила во второй экваториальной системе не меняются при суточном вращении небесной сферы. Поэтому именно она используется в звездных картах и атласах, в каталогах и списках небесных объектов.

Из рисунка 2.2 видно, что сумма часового угла и прямого восхождения для любого светила численно равна часовому углу точки весеннего равноденствия: 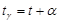. Этот угол принято называть местным звездным временем.

На практике используются и другие системы небесных координат. Например, при изучении движения тел солнечной системы обычно пользуются эклиптической координатной сеткой, где в качестве основного круга выступает эклиптика. Исследование структуры нашей Галактики удобнее всего производить в галактической системе небесных координат, в которой основным кругом является галактический экватор.

Экваториальные координаты (прямое восхождение 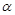и склонение 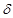) звезд, определяющие их положение на небесной сфере относительно небесного экватора, не зависят от положения наблюдателя на земной поверхности. В то же время вид самой небесной сферы, то есть, расположение ее элементов относительно истинного горизонта, зависит исключительно от географической широты 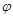места наблюдения, что находит свое выражение в теореме о высоте северного полюса мира над горизонтом. Напомним ее формулировку: высота северного полюса мира над горизонтом численно равна географической широте места наблюдения.

Поэтому изменение высоты 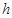и азимута 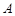небесного светила при суточном вращении небесной сферы и условия его видимости в разных местах Земли зависят не только от склонения светила 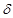, но и от географической широты 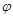места наблюдения на земной поверхности.

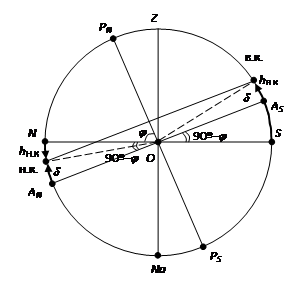
Рис. 1.3. Кульминации светила

Как мы знаем, при суточном вращении небесной сферы любое светило движется вдоль небесной параллели. При этом оно дважды в сутки пересекает небесный меридиан. Моменты пересечения светилом небесного меридиана называются кульминациями. Различают две кульминации светила – верхнюю и нижнюю. Верхняя кульминация, когда высота светила максимальна, происходит в южной стороне неба, над точкой юга 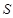на горизонте (рис. 1.3.). В момент нижней кульминации, происходящей вблизи точки севера 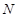на горизонте, высота светила имеет наименьшее значение. Высоту светила в верхней и нижней кульминациях можно рассчитать по формулам

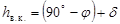,	(1.3)
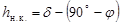.	(1.4)

В каждом месте земной поверхности с определенной географической широтой 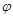, условия видимости небесных светил зависят от соотношения их склонения 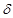и широты 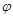. В зависимости от этого соотношения одни светила являются незаходящими в данном месте Земли, другие – невосходящими, третьи – восходят и заходят. Причем продолжительность их пребывания над горизонтом на протяжении суток и положение точек их восхода и захода опять-таки зависят от соотношения 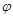и 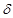(рис. 2.4). Условия видимости светил выводятся из формул, определяющих их высоту в верхней и нижней кульминации.

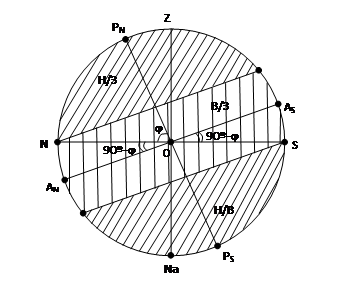
Рис. 1.4. Области незаходящих и невосходящих светил

Светила, которые даже в момент нижней кульминации не уходят под горизонт, то есть 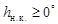, называются незаходящими. На основе этого определения можно записать условие незаходимости:

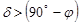(1.5)

Светила, которые даже в верхней кульминации не поднимаются над горизонтом, то есть 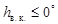, называются невосходящими. Для них справедливо условие невосходимости:

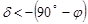(1.6)

Светила, верхняя кульминация которых происходит над горизонтом, а нижняя – под горизонтом, называются восходящими и заходящими. Условие восходимостии заходимости имеет вид:

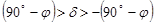(1.7)

Соотношение между и определяет также и расположение светила относительно зенита в момент верхней кульминации:

при верхняя кульминация светила происходит к югу от зенита;

при 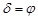в момент верхней кульминации светило проходит через точку зенита;

при 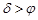верхняя кульминация светила наблюдается к северу от зенита.

Поэтому при вычислении зенитного расстояния 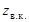или высоты 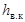светила в верхней кульминации, около числового результата необходимо проставить буквы S или N (юг или север), указывающие направления верхней кульминации. Кроме того, поскольку высота светил может быть положительной и отрицательной, перед числовым ее значением следует обязательно поставить соответствующий знак.

Для определения условий видимости небесных светил в южном полушарии Земли нужно помнить, что там над истинным горизонтом находится южный полюс мира, большинство видимых небесных светил принадлежит южной небесной полусфере и имеет отрицательное склонение ( 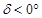), причем в нижней кульминации светила проходят через небесный меридиан над точкой юга или под ней. Поэтому при расчетах проще всего считать географическую широту 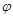точек южного полушария Земли и склонение 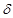небесных светил южной небесной полусферы положительными, а окончательному результату приписывать противоположное направление (N вместо S и наоборот). При вычислениях следует обязательно выполнять чертежи, которые дают наглядное представление о решаемых задачах и предохраняют от возможных ошибок.

Рассмотренные ранее условия видимости светил наглядно демонстрируются на модели небесной сферы. Помня, что всегда высота полюса мира 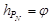, можно установить модель небесной сферы на определенную географическую широту 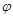и, укрепив насадки-светила в разных точках модели (в точках с различным склонением), увидеть при вращении модели различные суточные пути светил, плоскости которых наклонены к плоскости истинного горизонта под одним и тем же углом .

Изменяя склонение 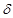насадок-светил, можно выяснить расположение точек их восхода и захода, условия их кульминации и условиях невосходящих и незаходящих светил.

Если же, не меняя склонения 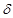светил, последовательно устанавливать модель небесной сферы на разную широту 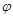, то можно убедиться в изменении условий видимости одних и тех же светил. Особенно рекомендуется обратить внимание на продолжительность пребывания над горизонтом различных широт светил, лежащих на небесном экваторе ( 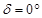). Это позволяет выяснить возможность наблюдений звезд на различных широтах областей северной и южной полусферы.

Установка модели небесной сферы для земного экватора ( 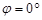; 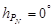) и северного географического полюса ( 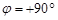; 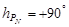) позволяет представить себе вид звездного неба на этих широтах.

Задания:

1. С помощью армиллярной сферы изучить вид и особенности суточного вращения небесной сферы на экваторе, тропиках, полярных кругах и географических полюсах Земли.

2. На модели небесной сферы отождествить величины, входящие в формулы зенитного расстояния и высоты небесных светил в моменты их верхней и нижней кульминации.

3. Вычислить зенитное расстояние и высоту в верхней и нижней кульминации звезд на земном экваторе, северном тропике, северном полярном круге, северном географическом полюсе и в городах:

№ варианта	Звезды	Города
1)	Капелла и Альфард	Санкт-Петербург и Махачкала
2)	Мирфак и Ригель	Пермь и Нальчик
3)	Шедар и Спика	Мурманск и Грозный
4)	Мицар и Фомальгаут	Петрозаводск и Астрахань
5)	Алголь и Сириус	Новгород и Майкоп
6)	Вега и Антарес	Москва и Владивосток
7)	Денеб и Мира	Архангельск и Южно-Курильск
8)	Дубхе и Менкар	Владимир и Биробиджан

4. Определить пояса географических широт, в которых эти звезды являются незаходящими и невосходящими.

5. Определить географическую широту мест земной поверхности, в которых те же звезды кульминируют в зените.

6. Определить склонение звезд, доступных наблюдениям в городах, указанных в пункте 4.

7. Изобразить на чертеже вид и направление вращения небесной сферы в произвольной точке поверхности южного полушария Земли.

8. Из анализа результатов пунктов 1-7 сформулировать выводы о причине различия вида звездного неба и об условиях видимости небесных светил в разных местах земной поверхности.

12 Следующая ⇒