ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.. Тема: «Числовые характеристики дискретной случайной величины». Решение.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.

Тема: «Числовые характеристики дискретной случайной величины»

Пример 1.Абитуриент сдаёт два вступительных экзамена: по математике и физике. Составить закон распределения случайной величины х – числа полученных пятёрок, если вероятность получения пятёрки по математике равна 0,8, а по физике – 0,6.

Решение.Обозначим А₁ и А₂ – события, заключающиеся в том, что и математика, и физика сданы на 5. Очевидно, возможные значения случайной величины х – числа сданных экзаменов есть 0, 1, 2, причём

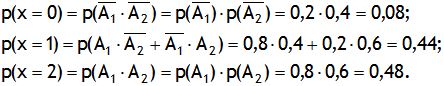
Полученные результаты сведём в таблицу:

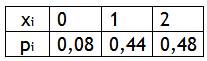
Проверка:

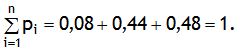
Пример 2. Дискретная случайная величина 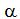– число гербов, выпавших при подбрасывании двух монет. Найти: 1) таблицу распределения величины 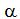; 2) функцию распределения; 3) P{ 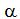<1,5}.

Решение.

Получаем таблицу распределения:

2) Функция распределения

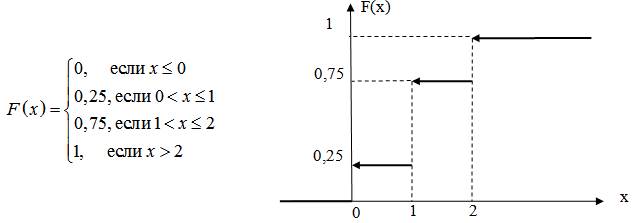
3) P( 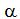<1,5) = F(1,5) = 0,75.

Пример 3. В лотерее выпущено 100 билетов. Разыгрывался один выигрыш в 50 у.е. и десять выигрышей по 10 у.е. Найти закон распределения величины X – стоимости возможного выигрыша.

Решение. Возможные значения величины X: x₁=0; x₂=10 и x₃=50. Так как "пустых" билетов 89, то p₁=0,89, вероятность выигрыша 10 у.е. (10 билетов) p₂=0,10 и для выигрыша 50 у.е. – p₃=0,01. Таким образом, закон распределения:

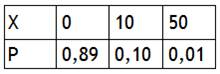
Легко проконтролировать: p₁+p₂+p₃ = 0,89+0,10+0,01 = 1.

Пример 4.Вероятность того, что покупатель ознакомился заранее с рекламой товара, равна 0,6 (р = 0,6). Осуществляется выборочный контроль качества рекламы путем опроса покупателей до первого, изучившего рекламу заранее. Составить ряд распределения количества опрошенных покупателей.

Решение. Согласно условию задачи р = 0,6. Отсюда q = 1-p = 0,4. Пусть m - число опрошенных покупателей. Подставив данные значения, получим: p(X=m) = p·q^m-1= 0,6·0,4^m-1и построим ряд распределения:

Пример 5.В связке из 3 ключей только один ключ подходит к двери. Ключи перебирают до тех пор, пока не отыщется подходящий ключ. Построить закон распределения для случайной величины ξ – числа опробованных ключей.

Решение. Число опробованных ключей может равняться 1, 2 или 3. Если испытали только один ключ, это означает, что этот первый ключ сразу подошел к двери, а вероятность такого события равна 1/3. Итак, P(ξ=1) = 1/3. Далее, если опробованных ключей было 2, т.е. ξ = 2, это значит, что первый ключ не подошел, а второй – подошел. Вероятность этого события равна 2/3·1/2 = 1/3. То есть, P(ξ=2) = 1/3. Аналогично вычисляется вероятность P(ξ=3) = 1/3. В результате получается следующий ряд распределения:

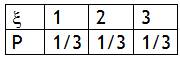
Пример 6. Построить функцию распределения F_ξ(x) для случайной величины ξ из предыдущей задачи.

Решение. Случайная величина ξ имеет три значения 1, 2, 3, которые делят всю числовую ось на четыре промежутка: (-∞,1), [1,2), [2,3), [3,+∞). Если x<1, то неравенство ξ≤x невозможно (левее x нет значений случайной величины ξ) и значит, для такого x функция F_ξ(x) = 0.

Если 1≤x<2, то неравенство ξ≤x возможно только если ξ=1, а вероятность такого события равна 1/3, поэтому для таких x функция распределения F_ξ(x) = 1/3.

Если 2≤x<3, неравенство ξ≤x означает, что или ξ=1, или ξ=2, поэтому в этом случае вероятность P(ξ<x) = P(ξ=1)+P(ξ=2) = 2/3, т.е. F_ξ(x) = 2/3.

И, наконец, в случае x≥3 неравенство ξ≤x выполняется для всех значений случайной величины ξ, поэтому P(ξ<x) = P(ξ=1)+P(ξ=2)+P(ξ=3) = 1, т.е. F_ξ(x) = 1.

Итак, мы получили следующую функцию:

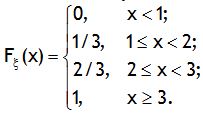
Пример 7.По мишени производится три выстрела, причем вероятность попадания при каждом выстреле равна 0,8. Рассматривается случайная величина X – число попаданий в мишень. Найти ее ряд распределения.

Решение. Случайная величина X принимает значения 0,1,2,3 с вероятностями, вычисленными по формуле Бернулли, где n = 3, p = 0,8 (вероятность попадания), q = 1-0,8 = 0,2 (вероятность непопадания).

Тогда

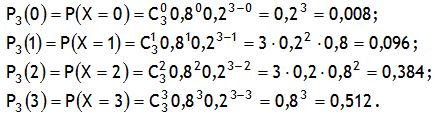
Таким образом, ряд распределения имеет следующий вид:

Задача 8. Пусть задан закон распределения случайной величины X:

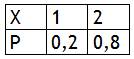
Найти математическое ожидание.

Решение.Математическое ожидание M(X) = 0,2·1+0,8·2 = 1,8.

Заметим, что вероятностный смысл математического ожидания – это среднее значение случайной величины.

Задача 9.Найти дисперсию случайной величины X со следующим законом распределения:

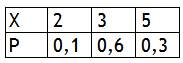
Решение.Здесь M(X) = 2·0,1+3·0,6+5·0,3 = 3,5.

Закон распределения квадрата величины X²:

M(X²) = 4·0,1+9·0,6+25·0,3 = 13,3.

Искомая дисперсия: D(X) = M(X²)-[M(X)]² = 13,3-3,5² = 1,05.

Дисперсия характеризует меру отклонения (рассеяния) случайной величины от её математического ожидания.

Задача 10. Пусть случайная величина задается распределением:

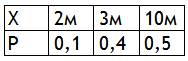
Найти её числовые характеристики.

Решение.M(X) = 2·0,1+3·0,4+10·0,5 = 6,4 м;

M(X²) = 2²·0,1+3²·0,4+10²·0,5 = 54 м²;

D(X) = M(X²)-[M(X)]² = 54-6,4² = 13,04 м²;

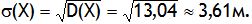
Задача 11.Закон распределения случайной величины задан таблично. Найти вероятности: р(х<2), р(х>4), р(2≤х≤4), математическое ожидание М(х), дисперсию D(x) и среднеквадратическое отклонение σ(x).

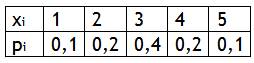
Решение.

р(х<2) = 0,1;

р(х>4) = 0,1;

р(2≤х≤4) = 0,2+0,4+0,2 = 0,8;

М(х) = 1·0,1+2·0,2+3·0,4+4·0,2+5·0,1 = 3;

D(x) = 1²·0,1+2²·0,2+3²·0,4+4²·0,2+5²·0,1-3² = 1,2;