
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа № 21.. Тема: Основные тригонометрические тождества. Методические материалы. Вычислить , если .. Вариант 1. Вариант 2
Практическая работа № 21.
Тема: Основные тригонометрические тождества
Цель работы: закрепить умение применять основные тригонометрические тождества, таблицу значений тригонометрических функций при упрощении и вычислении выражений.
Методические материалы
1. Вычислить , если .
1) Используя основное тригонометрическое тождество, получаем:

Т.к.  - 2 четверть
- 2 четверть 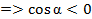 , получаем
, получаем 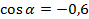
2) 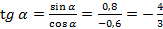 3)
3) 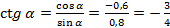
2. С помощью формул приведения найти значение выражения: а) 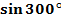 б)
б) 
а) 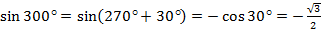
б) 
3. Упростить выражение: 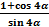
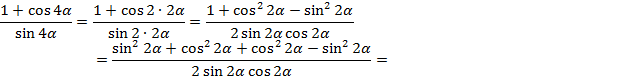




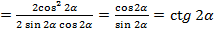
4. Доказать тождество: 

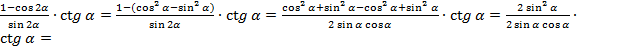


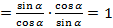
5. Найти значение выражения: 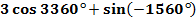
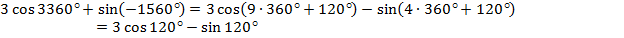
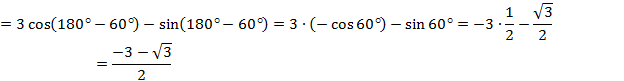
Основные тригонометрические тождества
o sin² α + cos² α = 1
o tg α · ctg α = 1
o tgα = sin α ÷ cos α
o ctgα = cos α ÷ sin α
o 1 + tg² α = 1 ÷ cos² α
o 1 + ctg² α = 1 ÷ sin² α
o Формулы сложения
o sin (α + β) = sin α · cos β + sin β · cos α
o sin (α - β) = sin α · cos β - sin β · cos α
o cos (α + β) = cos α · cos β - sin α · sin β
o cos (α - β) = cos α · cos β + sin α · sin β
o tg (α + β) = (tg α + tg β) ÷ (1 - tg α · tg β)
o tg (α - β) = (tg α - tg β) ÷ (1 + tg α · tg β)
o ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β - ctg α)
o ctg (α - β) = (ctg α · ctg β - 1) ÷ (ctg β + ctg α)
Вариант 1
1. Вычислите:
а) sin 150º; cos 240º; tg 135º; ctg 315º;
б) tg  ; ctg
; ctg  .
.
2. Вычислите:
а) 2 cos²α+1 при tgα=  ;
;
б) sin²х – 2 cos²х, если sin х= - 0,4;
в) 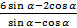 , если tg α = 3.
, если tg α = 3.
3. Найти значение выражения: (sin 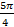 - cos
- cos 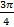 )·tg
)·tg 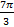 .
.
4. Дано: sinα =√ 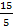
Найти: cosα; tgα; ctgα
5. Упростите выражения:
а) sinα · cosα · tgα;
б) sin²х- tgx· ctgx;
в) (1- sin²α) · tg ²α;
г)  .
.
Вариант 2
1. Вычислите:
а) sin 210º; cos 75º; tg 105º; ctg 250º;
б) tg 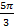 ; ctg
; ctg 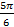 .
.
2. Вычислите:
а) 6 cos²α+1 при tgα=  ;
;
б) sin²х – 3 cos²х, если cos х= - 0,6;
в)  , если tg α = 4.
, если tg α = 4.
3. Найти значение выражения: 4 sin  + 3 tg²
+ 3 tg²  + ctg
+ ctg  + 2 cos
+ 2 cos  .
.
4. Дано: sinα =√ 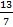
Найти: cosα; tgα; ctgα
5. Упростите выражения:
а) sinα · cosα ·ctgα;
б) tg x· ctg x - cos²х;
в) (1- cos α) (1+ cos α);
г) 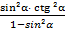 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|