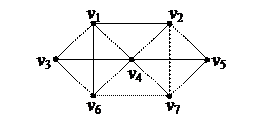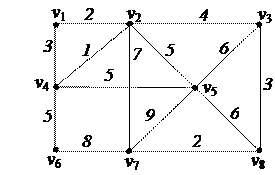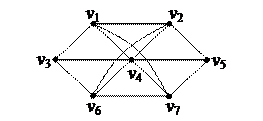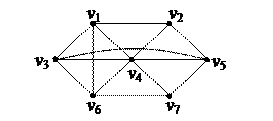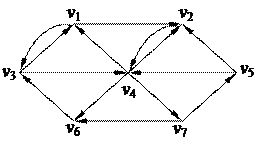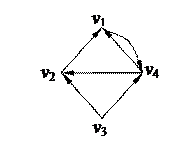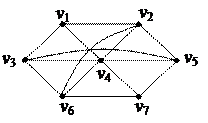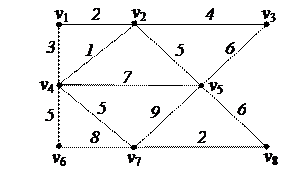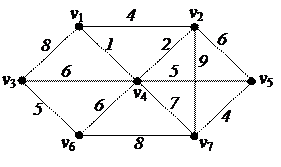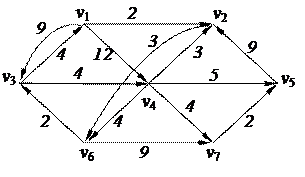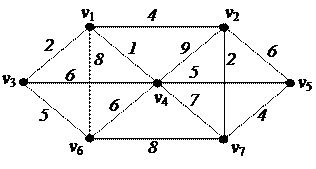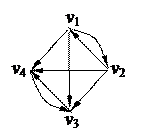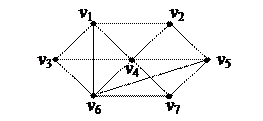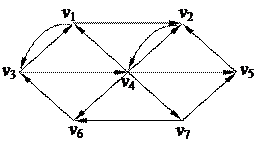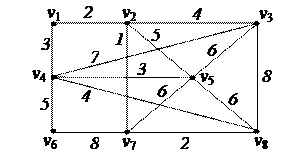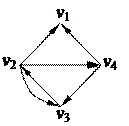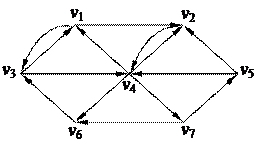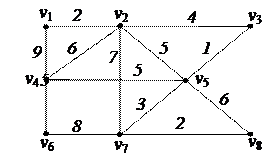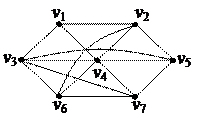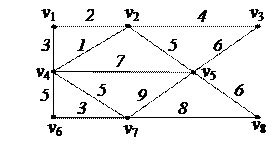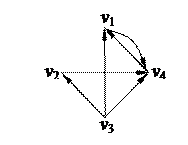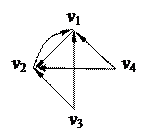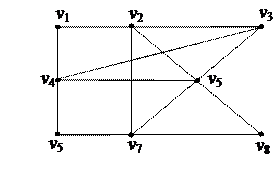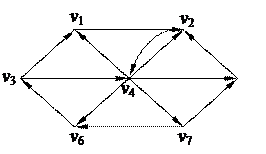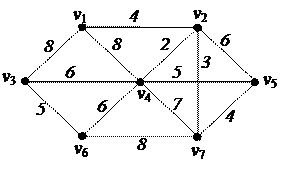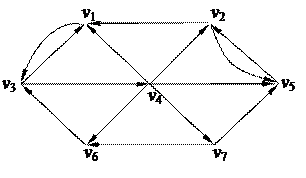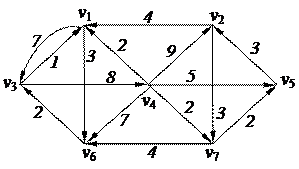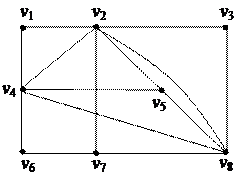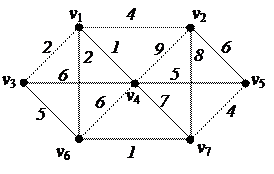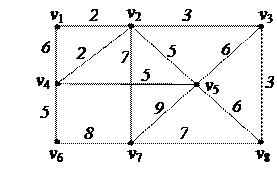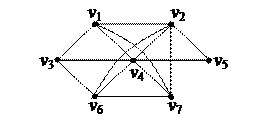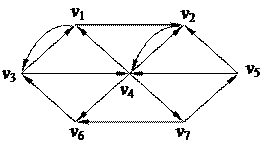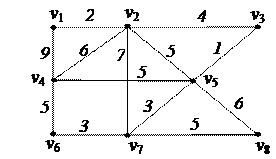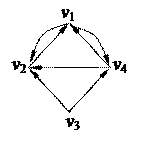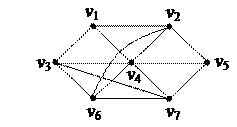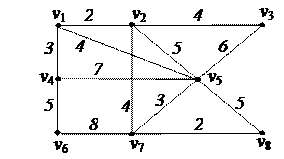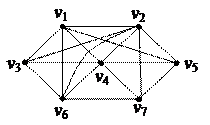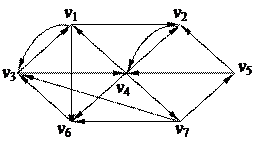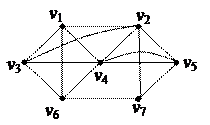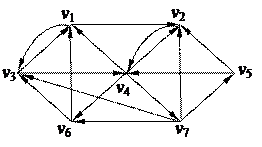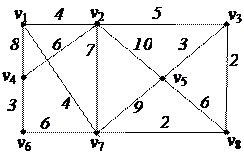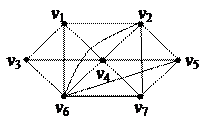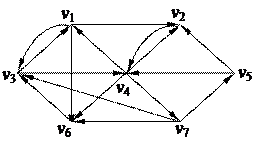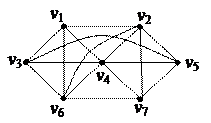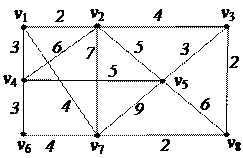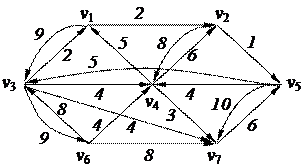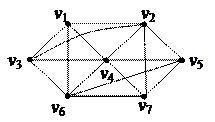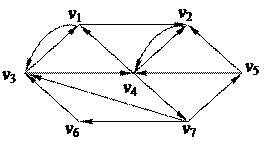Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

ВАРИАНТ №1. ВАРИАНТ №2. ВАРИАНТ № 3. ВАРИАНТ №4. ВАРИАНТ №5. ВАРИАНТ №6. ВАРИАНТ №7. ВАРИАНТ №8. ВАРИАНТ №9. ВАРИАНТ №10. ВАРИАНТ №11. ВАРИАНТ №12. ВАРИАНТ №13. ВАРИАНТ №14. ВАРИАНТ №15. ВАРИАНТ №16. ВАРИАНТ №17. ВАРИАНТ №18. ВАРИАНТ №19. ВАРИАНТ №20. ВАР

2.8 Практические задания по алгоритмам

ВАРИАНТ №1

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
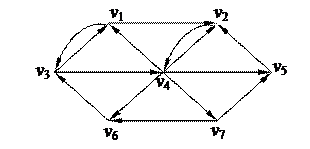2. С помощью алгоритма фронта волны найти минимальный путь из вершины v5 в v3 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
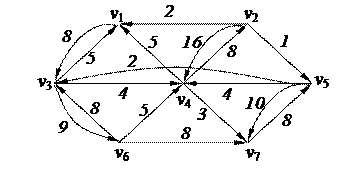
3. Найти минимальный путь в нагруженном орграфе из вершины v1 в v7 с помощью алгоритма Форда–Беллмана	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

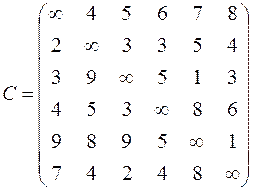
ВАРИАНТ №2

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
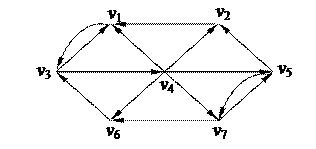2. С помощью алгоритма фронта волны найти минимальный путь из вершины v2 в v5 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
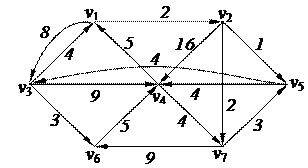
3. Найти минимальный путь в нагруженном орграфе из вершины v1 в v4 с помощью алгоритма Дейкстры	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

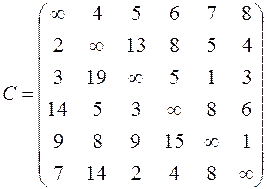
ВАРИАНТ № 3

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
2. С помощью алгоритма фронта волны найти минимальный путь из вершины v1 в v5 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
3. Найти минимальный путь в нагруженном орграфе из вершины v1 в v7 с помощью алгоритма Форда–Беллмана	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

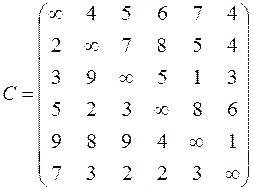
ВАРИАНТ №4

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
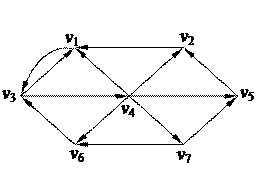2. С помощью алгоритма фронта волны найти минимальный путь из вершины v7 в v4 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний     v4	5. Найти минимальное остовное дерево в нагруженном графе   v6
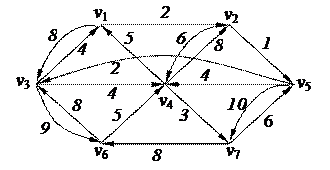
3. Найти минимальный путь в нагруженном орграфе из вершины v1 в v7 с помощью алгоритма Дейкстры	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

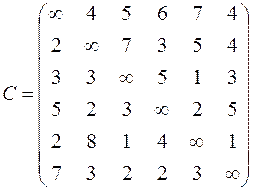
ВАРИАНТ №5

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
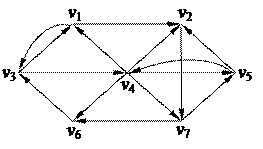2. С помощью алгоритма фронта волны найти минимальный путь из вершины v2 в v1 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
3. Найти минимальный путь в нагруженном орграфе из вершины v1 в v5 с помощью алгоритма Форда–Беллмана	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

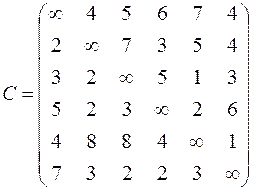
ВАРИАНТ №6

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
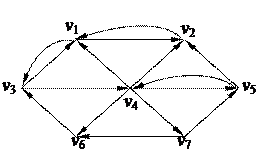2. С помощью алгоритма фронта волны найти минимальный путь из вершины v1 в v6 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
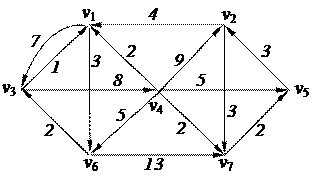
3. Найти минимальный путь в нагруженном орграфе из вершины v1 в v5 с помощью алгоритма Дейкстры	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

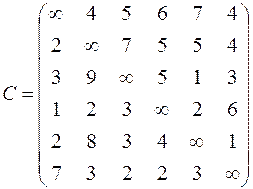
ВАРИАНТ №7

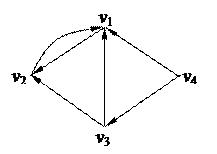1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
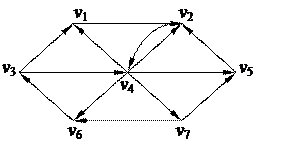
2. С помощью алгоритма фронта волны найти минимальный путь из вершины v1 в v3 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
3. Найти минимальный путь в нагруженном орграфе из вершины v1 в v7 с помощью алгоритма Форда–Беллмана	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

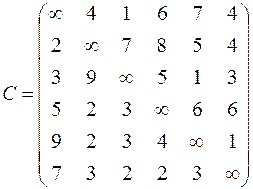
ВАРИАНТ №8

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
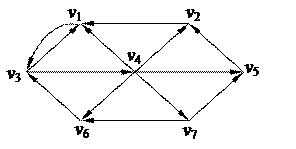
2. С помощью алгоритма фронта волны найти минимальный путь из вершины v5 в v7 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
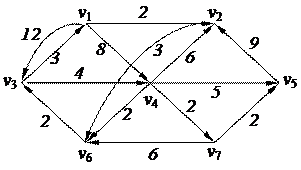
3. Найти минимальный путь в нагруженном орграфе из вершины v1 в v5 с помощью алгоритма Дейкстры	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

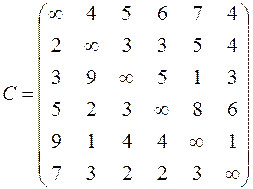
ВАРИАНТ №9

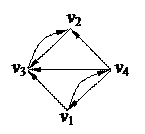1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
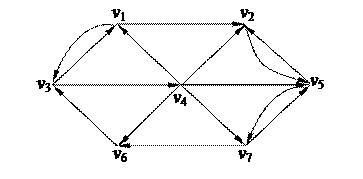2. С помощью алгоритма фронта волны найти минимальный путь из вершины v1 в v7 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
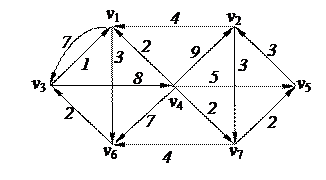
3. Найти минимальный путь в нагруженном орграфе из вершины v1 в v7 с помощью алгоритма Форда–Беллмана	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

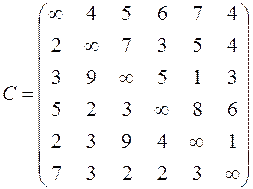
ВАРИАНТ №10

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
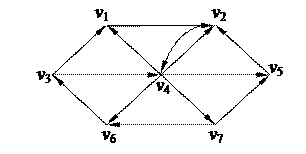2. С помощью алгоритма фронта волны найти минимальный путь из вершины v1 в v3 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
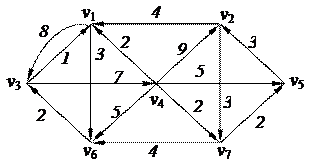
3. Найти минимальный путь в нагруженном орграфе из вершины v1 в v7 с помощью алгоритмаДейкстры	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

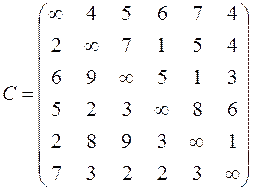
ВАРИАНТ №11

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
2. С помощью алгоритма фронта волны найти минимальный путь из вершины v5 в v1 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
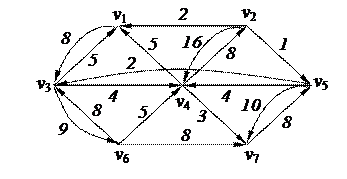
3. Найти минимальный путь в нагруженном орграфе из вершины v2 в v6 с помощью алгоритма Форда–Беллмана	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

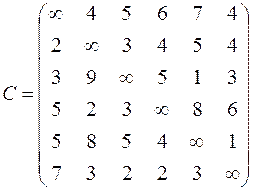
ВАРИАНТ №12

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
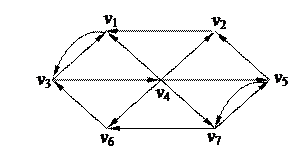
2. С помощью алгоритма фронта волны найти минимальный путь из вершины v3 в v7 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
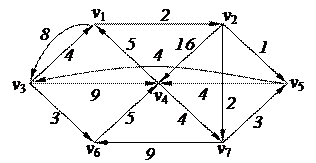
3. Найти минимальный путь в нагруженном орграфе из вершины v1 в v7 с помощью алгоритма Дейкстры	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

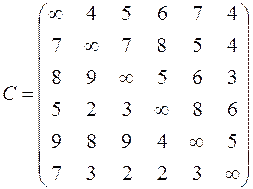
ВАРИАНТ №13

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
2. С помощью алгоритма фронта волны найти минимальный путь из вершины v1 в v7 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
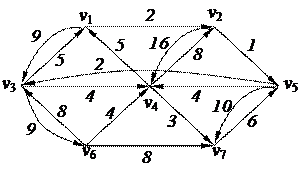
3. Найти минимальный путь в нагруженном орграфе из вершины v2 в v7 с помощью алгоритма Форда–Беллмана	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

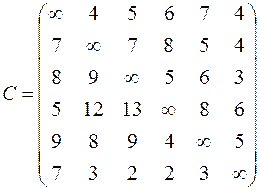
ВАРИАНТ №14

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
2. С помощью алгоритма фронта волны найти минимальный путь из вершины v7 в v1 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
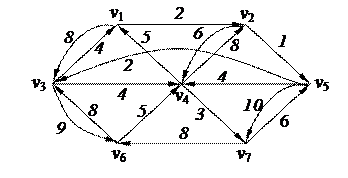
3. Найти минимальный путь в нагруженном орграфе из вершины v1 в v5 с помощью алгоритма Дейкстры	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

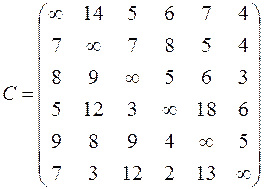
ВАРИАНТ №15

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
2. С помощью алгоритма фронта волны найти минимальный путь из вершины v2 в v6 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
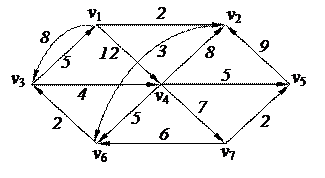
3. Найти минимальный путь в нагруженном орграфе из вершины v1 в v7 с помощью алгоритма Форда–Беллмана	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

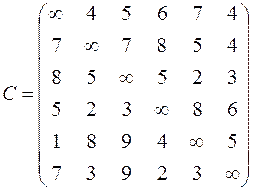
ВАРИАНТ №16

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
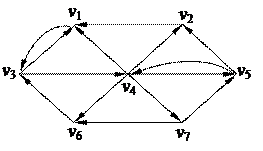2. С помощью алгоритма фронта волны найти минимальный путь из вершины v1 в v7 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
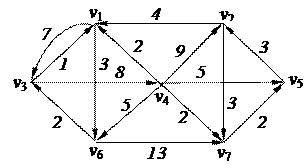
3. Найти минимальный путь в нагруженном орграфе из вершины v1 в v4 с помощью алгоритма  Дейкстры	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

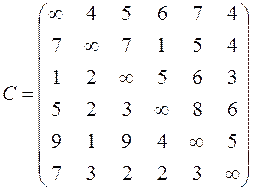
ВАРИАНТ №17

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
2. С помощью алгоритма фронта волны найти минимальный путь из вершины v1 в v6 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний v5	5. Найти минимальное остовное дерево в нагруженном графе
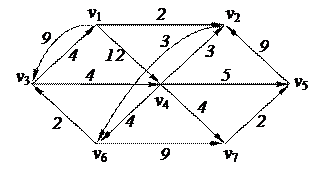
3. Найти минимальный путь в нагруженном орграфе из вершины v1 в v7 с помощью алгоритма Форда–Беллмана	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

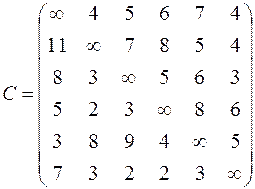
ВАРИАНТ №18

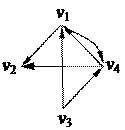
1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
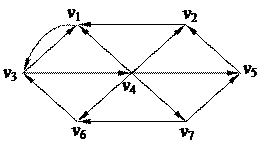2. С помощью алгоритма фронта волны найти минимальный путь из вершины v4 в v3 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
3. Найти минимальный путь в нагруженном орграфе из вершины v1 в v6 с помощью алгоритма  Дейкстры	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

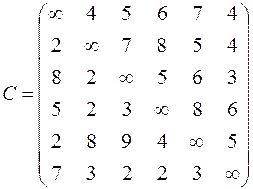
ВАРИАНТ №19

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
2. С помощью алгоритма фронта волны найти минимальный путь из вершины v1 в v4 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
3. Найти минимальный путь в нагруженном орграфе из вершины v4 в v6 с помощью алгоритма Форда–Беллмана	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

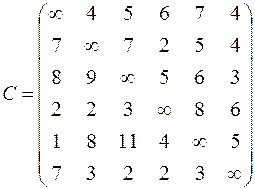
ВАРИАНТ №20

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
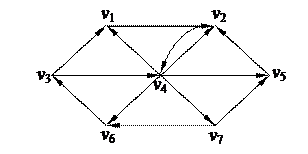
2. С помощью алгоритма фронта волны найти минимальный путь из вершины v1 в v6 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
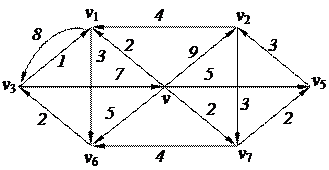
3. Найти минимальный путь в нагруженном орграфе из вершины v1 в v5 с помощью алгоритма  Дейкстры	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

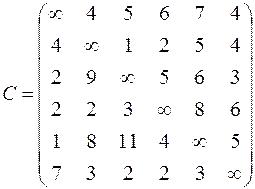
ВАРИАНТ №21

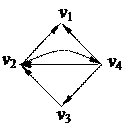
1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
2. С помощью алгоритма фронта волны найти минимальный путь из вершины v5 в v4 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
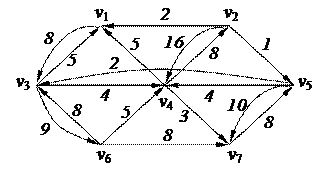
3. Найти минимальный путь в нагруженном орграфе из вершины v2 в v3 с помощью алгоритма Форда–Беллмана	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

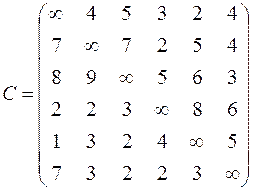
ВАРИАНТ №22

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
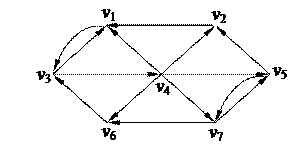2. С помощью алгоритма фронта волны найти минимальный путь из вершины v3 в v2 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
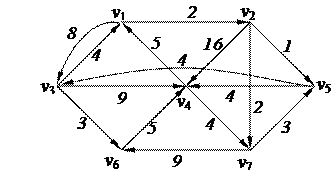
3. Найти минимальный путь в нагруженном орграфе из вершины v1 в v6 с помощью алгоритма  Дейкстры	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

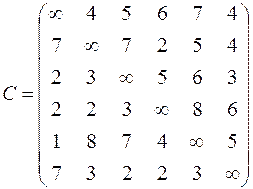
ВАРИАНТ №23

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
2. С помощью алгоритма фронта волны найти минимальный путь из вершины v2 в v7 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
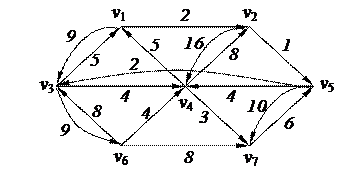
3. Найти минимальный путь в нагруженном орграфе из вершины v3 в v7 с помощью алгоритма Форда–Беллмана	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

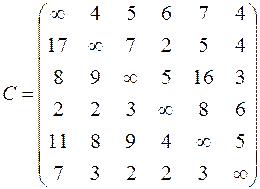
ВАРИАНТ №24

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
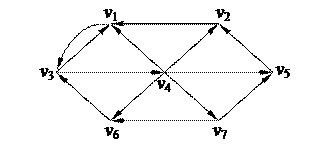
2. С помощью алгоритма фронта волны найти минимальный путь из вершины v7 в v3 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
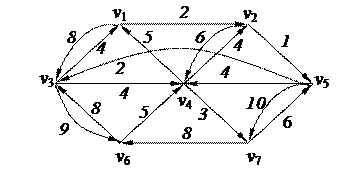
3. Найти минимальный путь в нагруженном орграфе из вершины v3 в v5 с помощью алгоритма  Дейкстры	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

ВАРИАНТ №25

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
2. С помощью алгоритма фронта волны найти минимальный путь из вершины v2 в v4 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
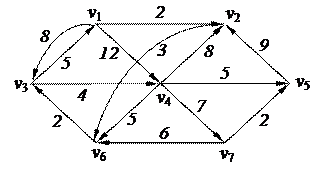
3. Найти минимальный путь в нагруженном орграфе из вершины v6 в v7 с помощью алгоритма Форда–Беллмана	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

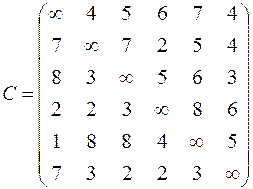
ВАРИАНТ № 26

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
2. С помощью алгоритма фронта волны найти минимальный путь из вершины v2 в v3 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
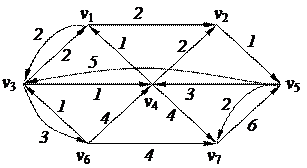
3. Найти минимальный путь в нагруженном орграфе из вершины v6 в v2 с помощью алгоритма Дейкстры	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

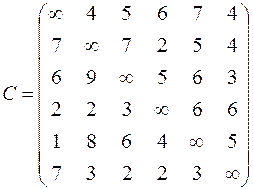
ВАРИАНТ № 27

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
2. С помощью алгоритма фронта волны найти минимальный путь из вершины v5 в v3 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
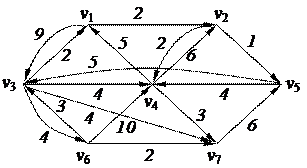
3. Найти минимальный путь в нагруженном орграфе из вершины v3 в v5 с помощью алгоритма Форда–Беллмана	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

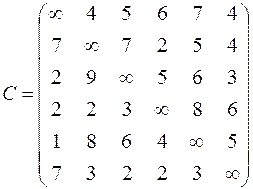
ВАРИАНТ № 28

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
2. С помощью алгоритма фронта волны найти минимальный путь из вершины v2 в v3 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
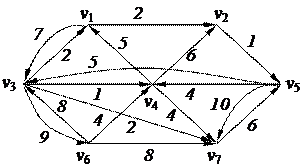
3. Найти минимальный путь в нагруженном орграфе из вершины v6 в v2 с помощью алгоритма Дейкстры	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

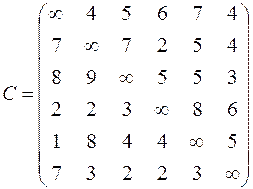
ВАРИАНТ № 29

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
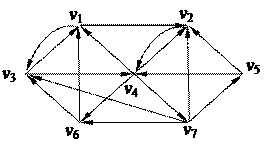
2. С помощью алгоритма фронта волны найти минимальный путь из вершины v5 в v3 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
3. Найти минимальный путь в нагруженном орграфе из вершины v1 в v7 с помощью алгоритма Форда–Беллмана	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

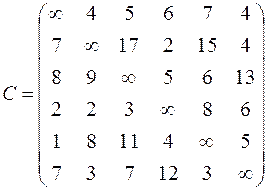
ВАРИАНТ № 30

1. Найти компоненты сильной связности орграфа	4. Найти Эйлерову цепь в графе
2. С помощью алгоритма фронта волны найти минимальный путь из вершины v2 в v6 в орграфе. Найти диаметр, радиус и центры с помощью матрицы минимальных расстояний	5. Найти минимальное остовное дерево в нагруженном графе
3. Найти минимальный путь в нагруженном орграфе из вершины v3 в v5 с помощью алгоритма Дейкстры	6. Решить задачу коммивояжера для нагруженного графа, заданного матрицей длин дуг.

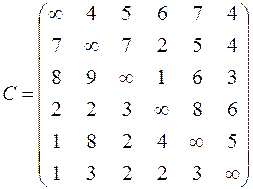
2.9 Практические задания

2.9.1. Изоморфизм графов

Задание 1.

а. Построить все попарно неизоморфные простые 4-вершинные графы.

б. Построить все попарно неизоморфные простые несвязные          5-вершинные графы, не имеющие изолированных вершин.

в. Построить все попарно неизоморфные 6-вершинные простые графы, состоящие из: 1) 4 компонент; 2) 3 компонент;                            3) 1 компоненты и имеющие 7 ребер и 2 висячие вершины.

г. Сколько существует попарно неизоморфных 6-вершинных простых графов со следующим набором степеней вершин:

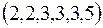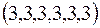1) ;2) ;3)?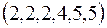

д. Для графов, полученных в пункте г, построить матрицы смежности и матрицы Кирхгофа.

Задание 2.

а.Сколько существует попарно неизоморфных деревьев, имеющих: 1) 6 ребер и 3 висячие вершины; 2) 6 ребер и 4 висячие вершины;

3) 7 ребер и 3 висячие вершины; 4) 8 ребер и 3 вершины степени 3?

б. Выяснить, какие наборы степеней вершин могут быть у простых связных 6-вершинных графов, имеющих 7 ребер, содержащих вершину степени 2 и вершину степени 3. Для каждого допустимого набора степеней вершин привести пример графа.

в. Доказать, что для любого 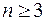 существует простой связный 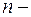вершинный граф, содержащий  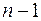вершин с нерав