
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Конспект урока по теме: «Первообразная. Интеграл»
Конспект урока по теме: «Первообразная. Интеграл»
Функция F(x) называется первообразной функции f(x) на некотором промежутке, если для всех х из этого промежутка Fˈ (x) = f(x).
Например, функция F (x) = Sin x является первообразной функции f (x) = Cos x, так как
(Sin x)ˈ = Cos x (смотреть формулы нахождения производных)
Функция F (x) = 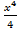 является первообразной функции f (x) = x 3 , так как
является первообразной функции f (x) = x 3 , так как
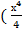 )ˈ =
)ˈ =  (х 4)ˈ =
(х 4)ˈ =  ∙ 4 х 3 = х3.
∙ 4 х 3 = х3.
Задача. Показать, что функция F (x) является первообразной функции f (x).
F (x) =  , f (x) = x 5
, f (x) = x 5
Чтобы решить этот пример надо от функции F (x) взять производную.
Операцию нахождения производной для заданной функции называют дифференцированием.
Обратную операцию нахождения первообразной для данной функции называют интегрированием.
Таблица первообразных
| Функция | Первообразная |
| x p, p ≠ - 1 | 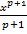 + c + c
|
 , x ˃ 0 , x ˃ 0
| Ln x + c |
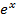
| 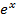 + c + c
|
| Sin x | - Cos x + c |
| Cos x | Sin x + c |
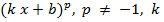 ≠ 0 ≠ 0
| 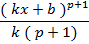
|
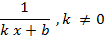
|  Ln ( k x + b) Ln ( k x + b)
|
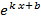 , k ≠ 0 , k ≠ 0
|  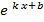 + c + c
|
| Sin ( k x + b), k ≠ 0 | 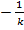 Cos ( k x + b) Cos ( k x + b)
|
| Cos ( k x + b), k ≠ 0 | 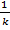 Sin ( k x + b) Sin ( k x + b)
|
Правила интегрирования
Пусть F (x) и G (x) – первообразные соответственно функций f (x) и g (x) на некотором промежутке. Тогда:
1) Функция F (x) ± G (x) является первообразной функции f (x) ± g (x);
2) Функция a F(x) является первообразной функции a f(x) ( а – постоянное число)
Задача 1. Найти первообразные функции
f (x) = x 2 + 3 Cos x
Используя правила интегрирования и таблицу первообразных для функций х р при р = 2 и для Cos x, находим одну из первообразных данной функции:
F (x) = 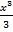 + 3 sin x + c
+ 3 sin x + c
Решить самостоятельно.
Найти первообразные функций:
1. f(x) = 2 x 5 – 3 x 2
2. f (x) = 5 x 4 + 2 x 3
3. f (x) = 6 x 2 – 4 x + 3
4. f (x) = 3 Cos x - 4 Sin x
5. f (x) = 5 Sin x + 2 Cos x
6. f (x) = e x - 2 Cos x
7. f(x) = 1 + 3 e x - 4 Cos x
Если в примере число, к нему добавляем х.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|