НОВЫЙ ВЗГЛЯД НА ЗАДАЧУ АНТИЧНОЙ МАТЕМАТИКИ

НОВЫЙ ВЗГЛЯД НА ЗАДАЧУ АНТИЧНОЙ МАТЕМАТИКИ

КВАДРАТУРА КРУГА

«ИССЛЕДОВАНИЕ ВОЗМОЖНОСТИ РЕШЕНИ

ЗАДАЧИ АНТИЧНОЙМАТЕМАТИКИ

КВАДРАТУРА КРУГА ОТ ОБРАТНОГО

1. РАВНОВЕЛИКОСТЬ КВАДРАТА И ШЕСТЕРЕНКИ

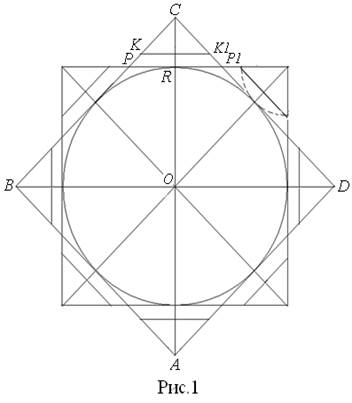
Около круга радиуса 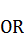(рис. 1), величину которого принимаем за единицу длины, опишем правильную восьмиконечную звезду 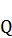, образованную из двух равных квадратов, один из которых квадрат ABCD

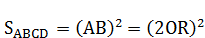Каждая сторона одного квадрата отсечёт от каждой прямоугольной вершины другого квадрата по треугольнику, один из которых треугольник .

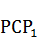Отсюда Радиусом 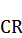из каждой прямоугольной вершины фигуры 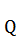опишем дуги на её стороны, а точки пересечения сторон и дуг соединим прямыми. В треугольнике 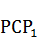такой прямой будет 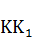. Пересекаясь с диагональю квадрата, прямая 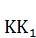образует точку 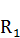. В фигуре 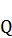каждый выступающий прямоугольный треугольник, равный треугольнику 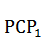_, будет делиться на две равновеликие фигуры, треугольник и трапецию, какими являются треугольник 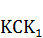и трапеция .

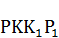Если удалить в фигуре 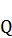все восемь одинаково выступающих прямоугольных треугольников, один из которых треугольник 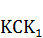, то получим фигуру 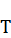– «шестерёнку» с выступающими трапециями по площади равной площади квадрата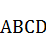

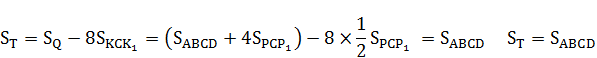
11. 2. КРУГАТУРА КВАДРАТА

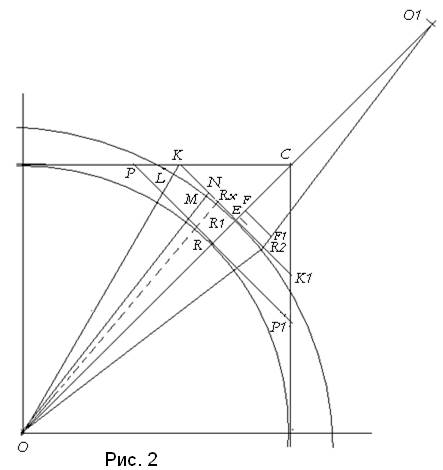
На рис. 2, который представляет фрагмент рис.1. Центр 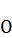соединим с точкой 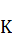. Получим треугольник 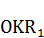, в котором проведём медиану .

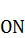Радиусом 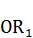проведём дугу, которая отсечёт от медианы 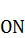отрезок 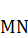, а от гипотенузы 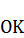– отрезок .

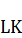Приводим расчёт полученных отрезков:

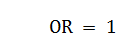(принимаем за 1)

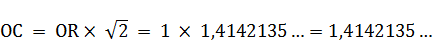
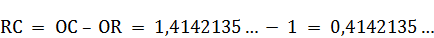
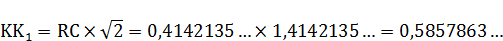
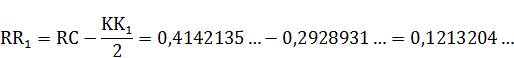
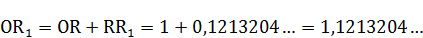
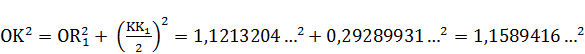
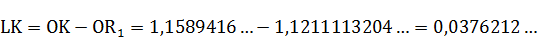
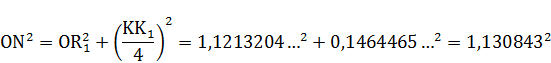
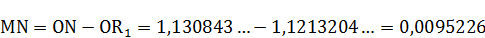
Радиус круга равновеликого квадрату 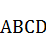примем условно за .

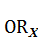Находим его арифметическую величину из равенства площадей условного круга с радиусом 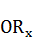и квадрата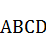

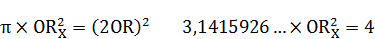
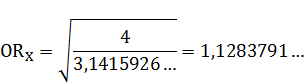
Условную точку 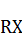расположим произвольно на отрезке 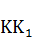и соединим её пунктирной прямой с центром O. Получим условный прямоугольный треугольник Арифметическую величину условного катета 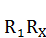, получим из решения

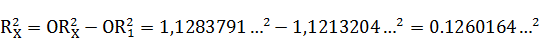
Эту же величину мы получим из пропорции составленную из величин отрезков, ранее полученных геометрически:

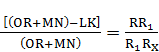
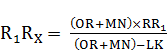
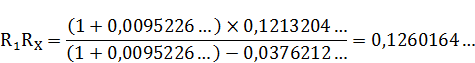
Арифметическую величину 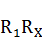выразим геометрическим отрезком. Отрезк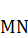и и 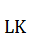перенесём на диагональ 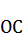радиусам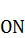и и 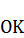. Отрезок 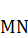отложится от точки 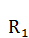до точки 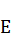, а отрезок 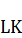от точки 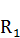до точки 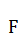. Затем отрезок 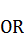положим на продолжение диагонали 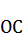так, чтобы началом отрезка 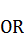была точка 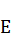, а концом – точка . Из точки 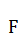построим перпендикуляр к 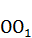, на котором отложим величину отрезка 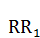, от точки 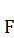до точки 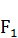. Через точки и 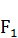проведём прямую до пересечения с прямой 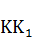в точке 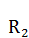. Таким образом, условная величина 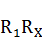выразилась геометрическим отрезком 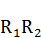. Полученную точку 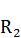соединим прямой с центром . 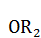Получим радиус круга равновеликого по площади квадрату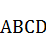

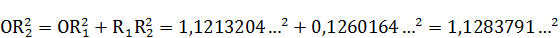
3. КВАДРАТУРА КРУГА

Если принять квадрат,

равновеликий по площади кругу с радиусом 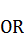за условный квадрат 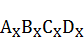, то получим пропорцию,

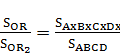
или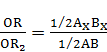

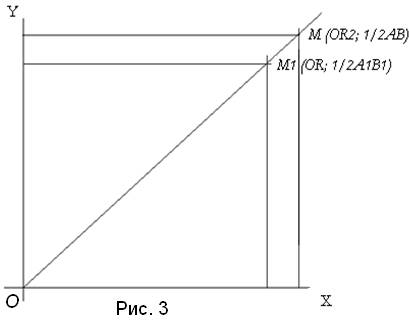
которую положим в систему координат (рис. 3), чтобы выразить услоную величину 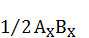геометрическим отрезком. Левую часть пропорции положим на ось абсцисс, правую – на ось ординат. Точк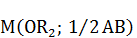и и 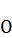дают луч, на котором абсциссой 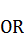отразится новая точка , проекция, которой на ось ординат, геометрически отразит ½ стороны искомого квадрата 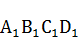, равновеликого по площади кругу радиуса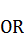

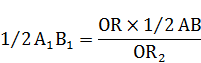
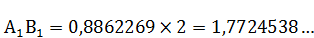
4. ДЛИНА ОКРУЖНОСТИ В ПРЯМОМ ОТРЕЗКЕ

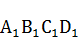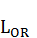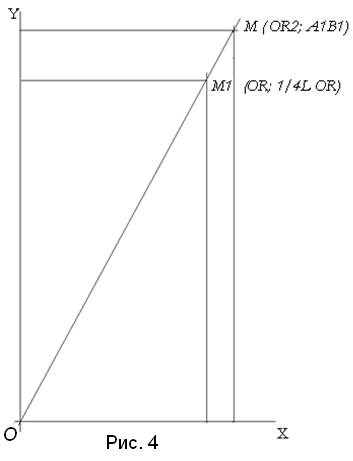
Нахождение стороны квадрата даёт возможность выразить – длину окружности круга радиуса 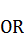прямым отрезком (рис.4).

Составим пропорцию:

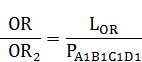
или

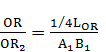
которую положим в систему координат.

Левую часть пропорции, положим на ось абсцисс, правую – на ось ординат.

Точк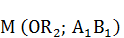и и 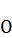дают луч, на котором абсциссой 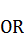образуется новая точка 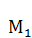, проекция которой на ось ординат геометрически отразит прямым отрезком .

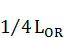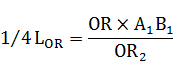
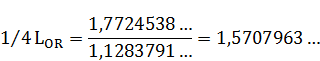
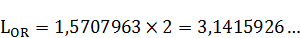
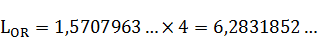
В свою очередь, 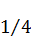длины окружности круга, радиуса 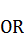_, тоже выражена прямым отрезком A₁B₁, что видно из Рис. 4

Если расчёт задачи вести на большее количество знаков, то сторона квадрата 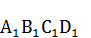будет равна

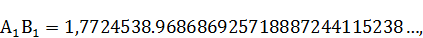
а площадь, равновеликого кругу квадрата, будет равна

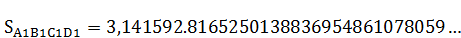» [9, с. 97 – 100].

5. ВЫВОД ФОРМУЛ ДЛЯ ЧИСЕЛ 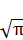И

НА ОСНОВЕ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ

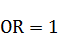
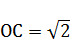
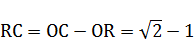
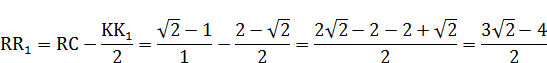
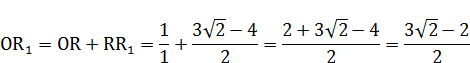
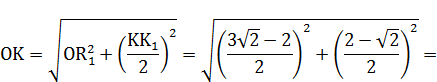
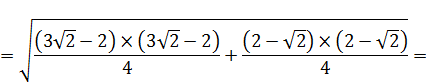
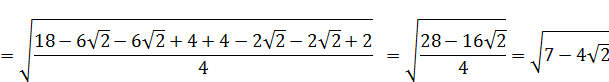
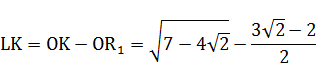
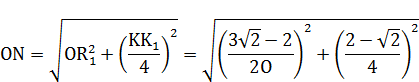
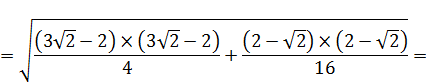
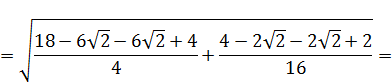
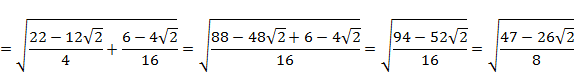
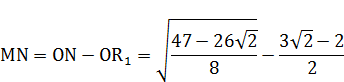
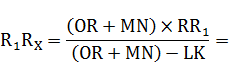
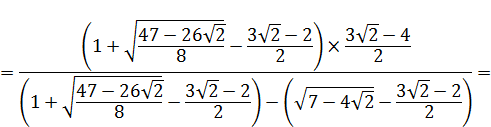
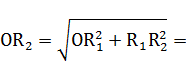
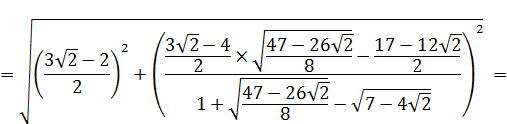
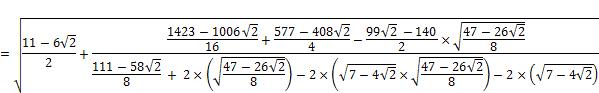
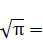
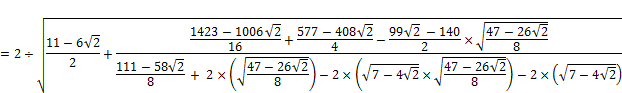
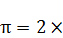
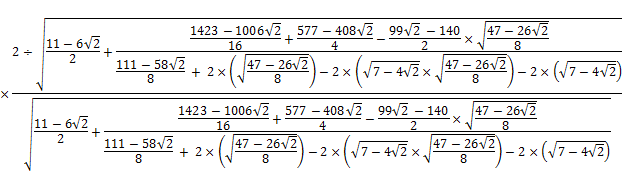
6. РАСЧЕТ ЧИСЕЛ 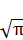И НА ОСНОВЕ ВЫВЕДЕННЫХ ФОРМУЛ

Промаркируем в формуле, составляющие формулу элементы:

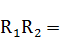
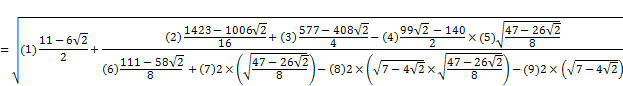
Произведем поэтапный расчет промаркированных элементов:

(1)

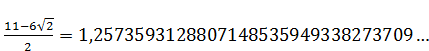
(2)

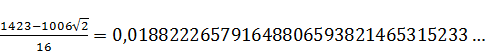
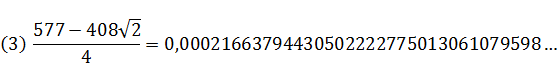
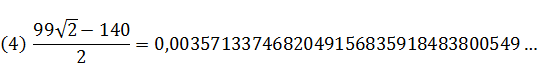
(5) …

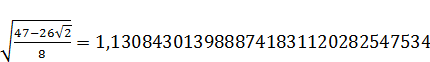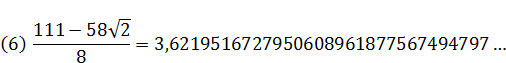
(7)

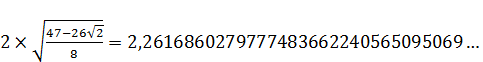
(8)

…

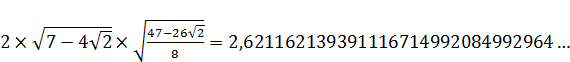
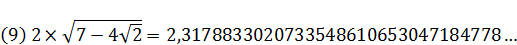
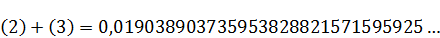
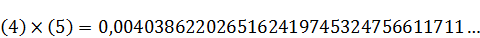
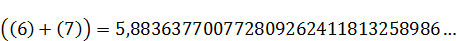
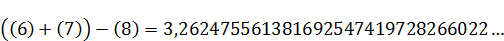
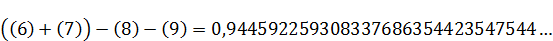
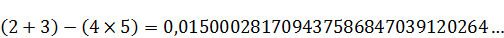
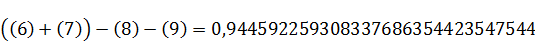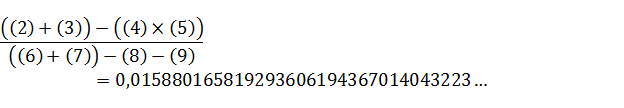
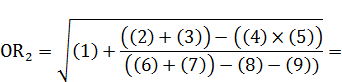
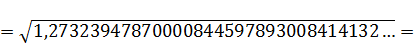
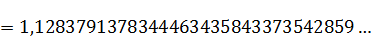
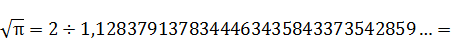
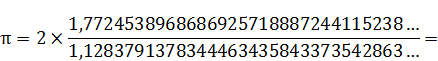
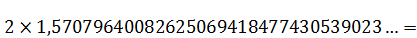
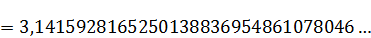
ВЫВОД

Выбранный подход к решению задачи античной математики, позволил, кроме основной цели, - решения Квадратуры круга, выйти на решение Кругатуры квадрата, выражение длины окружности прямым отрезком. Также обратите внимание, на тот факт, что длина окружности, круга , получилась равной периметру сторон квадрата 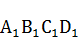, произвольно, - без специальных на то построений. Геометрические построения, позволили вывести формулы для чисел 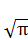и π. Формулы данных чисел конечны, а иррациональность чисел 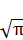и π определяет число 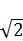, на котором зиждется геометрическое построение Квадратуры круга.

Количество знаков, получаемых при расчете чисел 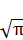и π, зависит от количества взятых для расчета знаков числа - .

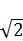Хочу заметить, что проще рассчитать число по формулам, взятым из алгоритма геометрического построения, чем рассчитывать по выведенным формулам. Во всяком случае, так было проще для меня. Приведенные результаты для

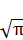и π на 32 знака в конце геометрического решения квадратуры круга, были рассчитаны именно по формулам алгоритма геометрического построения.

Читатели могут задать вопрос: “Почему автор выдает информацию, что решение совпадает на 8 знаков, при этом выдает результат числа π, равный

3,1415928…, где совпадение на 7 знаков?”

Дело в том, что по условию задачи требуется построить сторону квадрата, площадь которого равна площади заданного круга, т. е. построение идет на результат построения отрезка равного 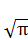, и данный результат и совпадает на 8 знаков с числом Лудольфа.

Результат построенного отрезка: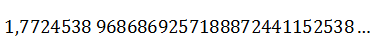

√(из лудольфова числа) : 1,7724538 50905516027298167483341…

Девятый знак, определяет, быть ли числу - 3,1415926… или 3,1415928…

CПИСОК ЛИТЕРАТУРЫ

[1] Бобынин В.В. Математика Древних Египтян: по папирусу Ринда. —

— Москва: Книжный дом «Либрком», Издание второе, 2012. — 208 с.

(Физико- математическое наследие: математика (история математики).)

ISBN 978 – 5 – 397 – 02749 – 6

[2] Прасолов В.В. Три классические задачи на построение: удвоение куба, трисекция угла, квадратура круга. — Москва: «Наука». Гл. ред. Физ.-мат. лит., 1992. — 80 с. (Популярные лекции по математике; Вып. 62)

ISBN 5 – 02 – 014849 – 0

[3] Рудио Ф., перевод Бернштейн С.Н. О квадратуре круга с приложением истории вопроса. — Москва, Ленинград: Объединенное научно - техническое издательство ОНТИ НКТП СССР, издание третье, 1936. — 237 с.

(Классики естествознания Архимед, Гюйгенс, Ламберт, Лежандр)

[4] Брокгауз Ф.А., Ефрон И.А. Энциклопедический словарь, Том 14^а. — — С – Петербург: Типо – Литография П.А. Ефрона, Прачешный переулок № 6, 1895. — 960 с.

[5] Прохоров А.М. Большая Советская энциклопедия, Том 11. — Москва:

Издательство «СОВЕТСКАЯ ЭНЦИКЛОПЕДИЯ», 1973. — 680 с.

[6] Осипов Ю.С. Большая Российская энциклопедия, Том 13. — Москва: «БОЛЬШАЯ РОССИЙСКАЯ ЭНЦИКЛОПЕДИЯ», 2008. — 783 с.

ISBN 978 – 5 – 85270 – 344 – 6

[7] Перельман Я.И. Квадратура круга. — Ленинград: Издание «Дом занимательной науки», 1941. — 25 с.

[8] Савин А.П. Энциклопедический словарь юного математика.—Москва:

«Педагогика», 1989. — 352 с.

ISBN 5 – 7155 – 0218 – 7

[9] Дениченко С.Н., Дениченко Л.В. Исследование возможности решения задачи античной математики Квадратура круга от обратного. /Журнал научных публикаций аспирантов и докторантов № 12 декабрь, 2011, c. 97 – 100. — Курск: Редакция журнала научных публикаций аспирантов и докторантов, 2011,— 114 с. ISSN 1991- 3087

Интернет - адрес статьи: «Исследование возможности решения задачи античной математики Квадратура круга от обратного» —

www.jurnal.org/articles/2011/mat9.html — Дата доступа: 30.09.2012

[10] Интернет ресурс – Википедия. — ru.wikipedia/wiki/Формула_Эйлера — дата доступа 22.09.2012

[11] Прохоров А.М. Большой энциклопедический словарь. — 2-е изд., перераб. и доп. — М., “Большая Российская энциклопедия”; СПб.: “Норинт”,

2011. — 1456 с.: ил.

ISBN 5 – 85270 – 160 – 2

ISBN 5 – 7711 – 0004 – 8

(Большой энциклопедический словарь (БЭС) – универсальное справочное издание, охватывающее все области современного знания. Второе, существенно обновленное издание содержит около 80 000 статей, в том числе 20 000 биографий. Сведения в БЭС дано по состоянию на 1999 – 2000 гг.)

ПРИМЕЧАНИЕ

¹Витковский Вас. Вас. (1856 – 1924), рос. геодезист, ген.- лейтенант. Проф. геод. отделения Академии Генштаба (с 1897). Автор уч. руководства по топографии, геодезии и картографии

[11, с. 209]

² Менделеев Дм. Ив. (1834 – 1907), рос. химик, разносторонний ученый, педагог. Открыл (1869) периодич. закон хим. элементов — один из основных законов естествознания. Оставил св. 500 печатных трудов, среди к - рых класич. “Основы химии” (ч. 1 – 2, 1869 – 71, 13 изд. 1947) – первое стройное изложение неорганической химии. Автор фундаментальных иссл. по химии, хим. технологии, физике, метрологии, воздухоплаванию, метеорологии, с. х - ву, экономике, нар. просвещению и др., тесно связанных с потребностями развития России. Заложил основы теории р – ров, предложил пром. способ фракц. разделения нефти, изобрел вид бездымного пороха, пропагандировал использования минер. Удобрений, орошения засушливых земель. Один из инициаторов создания Рус. хим. об – ва (1868; ныне Хим. об – во им. М.).

Проф. Петерб. ун-та (1865 – 90), ушел в отставку в знак протеста против притеснения студенчества. С 1876 ч-к. Петерб. АН, в 1880 выдвигался в академики, но был забаллотирован, что вызвало резкий обществ. протест.

Организатор и первый дир. (1893) Гл. палаты мер и весов (ныне ВНИИ метрологии им. М.)

[11, с. 716].