- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Проекция вектора на ось. ax=a×cosa.. Таблица часто применяемых косинусов.. Действия над векторами.
Проекция вектора на ось
Проекция вектора на ось равна произведению модуля вектора на косинус угла между вектором и осью:
ax=a×cosa.
Определение вектора по его проекциям:
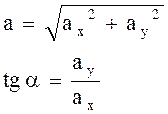
где a - угол между вектором  и осью x.
и осью x. 
Геометрический смысл проекции вектора на ось: проекция вектора на ось равна разности координат конца и начала вектора:
 ах=х2-х1
ах=х2-х1
ау=у2-у1
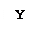 | |||
 | |||
 |
Если выражение справедливо для векторов, то оно справедливо и для проекций этих векторов на ось.
Пример:
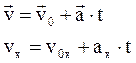
Таблица часто применяемых косинусов.
 |
cos 00 = 1
cos300 = 0,866 cos(900-a) = sin a
cos450 = 0,7 cos(900+a) =-sin a
cos600 = 0,5 cos(1800-a)=-cos a
cos900 = 0
cos1800=-1
Действия над векторами.
Чтобы найти сумму нескольких векторов, надо параллельным переносом этих векторов совместить начало каждого последующего вектора, начиная со второго, с концом предыдущего вектора, тогда вектор, который выходит из начала первого вектора и приходит в конец последнего, является вектором суммы. Следовательно, чтобы найти сумму двух векторов а и bнадо параллельным переносом вектора b совместить его начало с концом вектора а, тогда вектор суммы сбудет выходить из начала вектора а и приходить в конец вектора b. Это правило сложения векторов называется правилом треугольника.
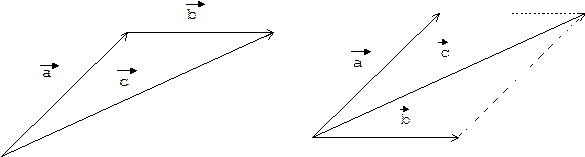
 Из правила треугольника непосредственно вытекает другое правило нахождения суммы векторов - правило параллелограмма.
Из правила треугольника непосредственно вытекает другое правило нахождения суммы векторов - правило параллелограмма.
Чтобы найти сумму двух векторов, надо параллельным переносом совместитьих начала и на этих векторах, как на сторонах, построить параллелограмм. Диагональ параллелограмма, выходящая из общего начала векторов, будет являться вектором суммы.
Пример. Даны векторы а,b,с,d. Найти сумму этих векторов - вектор Т.
Согласно данному выше определению параллельным переносом векторов совместим начало каждого последующего вектора, начиная со второго с концом предыдущего.
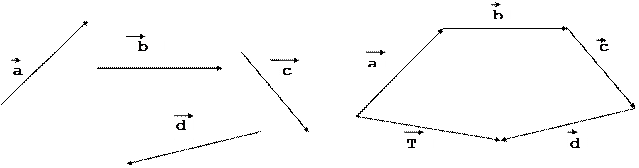
Искомый вектор Т будет выходить из начала первого вектора а и приходить в конец последнего вектора d.
|
|
Действие вычитания векторов обратно действию сложения. Если даны два вектора с и а, то разностью (с - а) называется такой вектор b, который с вектором а в сумме составляет вектор с. Для построения вектора разности b = (с - а) надо вектора с и а свести началами в одну точку, тогда вектор b соединит концы этих векторов и будет направлен в сторону уменьшаемого ( с ).
   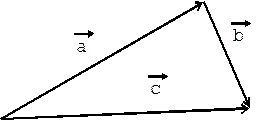
|
Теорема косинусов:
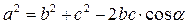
Теорема синусов:
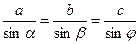
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|