
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Производная и дифференциал. Дифференцирование явных функций. Пусть мы имеем функцию
1. Производная и дифференциал
(Повторение)
1.1. Дифференцирование явных функций
Понятие производной – важнейшее понятие математического анализа, наряду с понятием интеграла.
Пусть мы имеем функцию
y = f(x)
определенную в некотором промежутке. При каждом значении аргумента х из этого промежутка функция y = f(x) имеет определенное значение.
Пусть аргумент х получил некоторое (положительное или отрицательное – безразлично) приращение Dх. В этом случае функция у получит некоторое приращение Dу. Таким образом:
при значении аргумента х будем иметь y = f(x),
при значении аргумента х + Dх будем иметь у + Dу = f(х + Dх).
Найдем приращение функции Dу:
Dу = f(x + Dx) – f(x).
Составим отношение приращения функции к приращению аргумента:
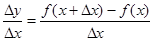 .
.
Найдем предел этого отношения при Dx ® 0. Если этот предел существует, то его называют производной данной функции f(x) и обозначают 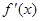 . Таким образом, по определению
. Таким образом, по определению
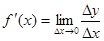
или
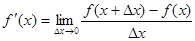 .
.
Следовательно, производной данной функции у = f(x) по аргументу х называется предел отношения приращения функции Dу к приращению аргумента Dх, когда последнее произвольным образом стремится к нулю.
Отметим, что в общем случае для каждого значения х производная 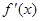 имеет определенное значение, т.е. производная является также функцией от х.
имеет определенное значение, т.е. производная является также функцией от х.
Наряду с обозначением 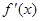 для производной употребляются и другие обозначения
для производной употребляются и другие обозначения 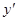 ,
, 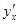 ,
, 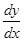 . Конкретное значение производной при x = a обозначается
. Конкретное значение производной при x = a обозначается 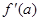 или
или 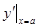 . Операция нахождения производной от функции f(x) называется дифференцированием этой функции.
. Операция нахождения производной от функции f(x) называется дифференцированием этой функции.
Механический смысл производной: производная пути по времени 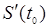 есть скорость точки в момент
есть скорость точки в момент 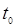 :
: 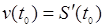 .
.
Геометрический смысл производной: производная 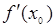 есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой
есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой 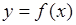 в точке
в точке 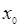 , то есть
, то есть 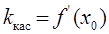 .
.
Уравнение касательной к кривой 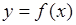 в точке
в точке 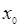 :
:
 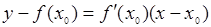 . .
|
Нормалью к кривой в точке 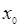 называется прямая, перпендикулярная касательной, проходящей через точку
называется прямая, перпендикулярная касательной, проходящей через точку 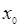 , тогда
, тогда

и уравнение нормали имеет вид
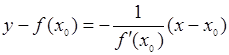
|
(здесь 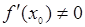 ).
).
Определение. Если функция
у = f(х)
имеет производную в точке 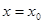 , т.е. если существует
, т.е. если существует
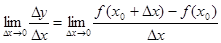 ,
,
то при данном значении 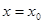 функция дифференцируема или (что равносильно этому) имеет производную.
функция дифференцируема или (что равносильно этому) имеет производную.
Если функция дифференцируема в каждой точке отрезка [a: b] или интервала (a; b), то она дифференцируема на отрезке [a; b] или соответственно в интервале (a; b).
Теорема. Если функция у = f(х) дифференцируема в некоторой точке 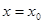 , то она в этой точке непрерывна.
, то она в этой точке непрерывна.
Таким образом, в точках разрыва функция не может иметь производной. Обратное заключение не верно, т.е. из того, что в какой-нибудь точке 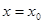 функция у = f(х) непрерывна, еще не следует, что в этой точке она дифференцируема: функция f(x) может и не иметь производной в точке
функция у = f(х) непрерывна, еще не следует, что в этой точке она дифференцируема: функция f(x) может и не иметь производной в точке 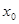 .
.
Например, рассмотрим функцию 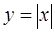 , в точке
, в точке 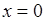 она непрерывна, но не дифференцируема
она непрерывна, но не дифференцируема
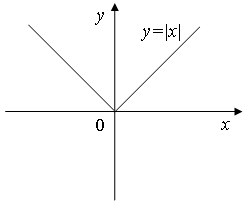
Докажем, что функция 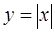 не дифференцируема в точке
не дифференцируема в точке 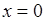 .
.
Производная функции (если она существует) равна
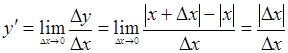 .
.
Очевидно, что при 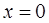 производная не существует, так как отношение
производная не существует, так как отношение 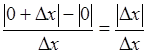 равно 1 при
равно 1 при 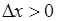 и
и 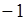 при
при 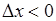 , то есть не имеет предела при
, то есть не имеет предела при 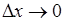 (ни конечного, ни бесконечного). Геометрически это означает отсутствие касательной к кривой в точке
(ни конечного, ни бесконечного). Геометрически это означает отсутствие касательной к кривой в точке 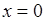 .
.
Приведем далее основные формулы и правила дифференцирования.
Формулы дифференцирования основных функций.
1. 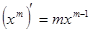 . 11.
. 11. 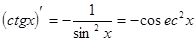 .
.
2. 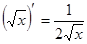 . 12.
. 12. 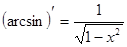 .
.
3. 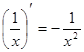 . 13.
. 13. 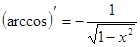 .
.
4. 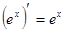 . 14.
. 14. 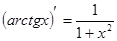 .
.
5. 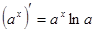 . 15.
. 15. 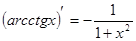 .
.
6. 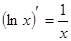 . 16.
. 16. 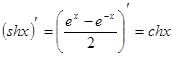 .
.
7. 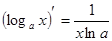 . 17.
. 17. 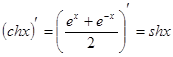 .
.
8. 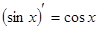 . 18.
. 18. 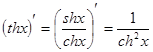 .
.
9. 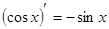 . 19.
. 19. 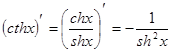 .
.
10. 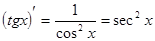 .
.
Основные правила дифференцирования.
Пусть С – постоянная, u = u(x) и v = v(x) – функции, имеющие производные.
Тогда:
1) 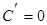 ;
;
2) 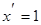 ;
;
3) 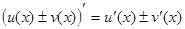 ;
;
4) 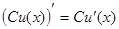 ;
;
5) 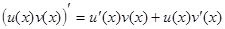 ;
;
6) 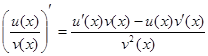 ;
;
7) правило дифференцирования сложной функции.
Пусть дана сложная функция y = f(x), т.е. такая, что ее можно представить в виде:
y = F(u), u = j(x)
или y = F(j(x)). В выражении y = F(u) переменную u называют промежуточной переменной.
Теорема. Если функция u = j(x) имеет в некоторой точке х производную 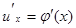 , а функция y = F(u) имеет при соответствующем значении u производную
, а функция y = F(u) имеет при соответствующем значении u производную 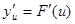 , то сложная функция y = F(j(x)) в указанной точке х также имеет производную, которая равна
, то сложная функция y = F(j(x)) в указанной точке х также имеет производную, которая равна 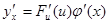 , где вместо u должно быть подставлено выражение u = j(x). Коротко
, где вместо u должно быть подставлено выражение u = j(x). Коротко
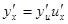 ,
,
т.е. производная сложной функции равна произведению производной данной функции по промежуточному аргументу u на производную промежуточного аргумента по х.
Если функция y = f(x) такова, что ее можно представить в виде
y = F(u), u = j(v), v = y(x),
то нахождение производной 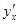 производится путем последовательного применения указанной теоремы.
производится путем последовательного применения указанной теоремы.
По указанному правилу имеем 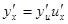 . Применяя эту же теорему для нахождения
. Применяя эту же теорему для нахождения 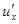 , будем иметь
, будем иметь 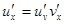 . Подставляя выражение
. Подставляя выражение 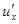 в предыдущее равенство, получаем
в предыдущее равенство, получаем
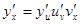
или
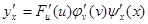 .
.
Пример 1. Исходя из определения производной, найти производную функции 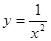 .
.
Находим приращение функции
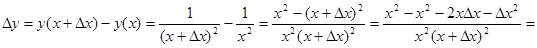
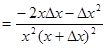 .
.
Находим отношение приращения функции к приращению аргумента:
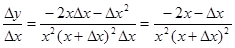 .
.
Найдем предел этого отношения при Dх ® 0
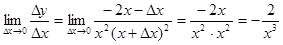 .
.
Следовательно, по определению производной 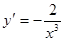 .
.
Пример 2.Исходя из определения производной, найти производную функции y = 5 sin x +3 cos x.
Находим приращение функции:
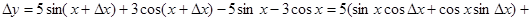
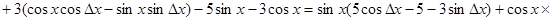
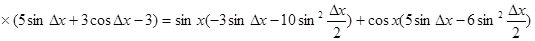 .
.
Отсюда
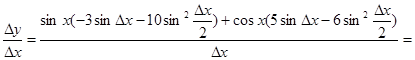
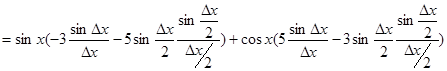 .
.
Таким образом,
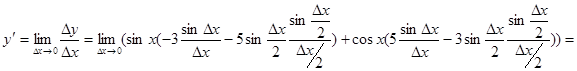
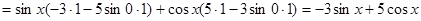 .
.
Итак, 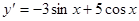 .
.
Пример 3. Исходя из определения производной, найти производную функции 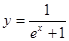 .
.
Находим
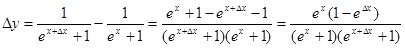 .
.
Отсюда
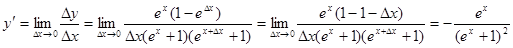 .
.
Итак, 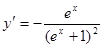 .
.
Применяя формулы и правила дифференцирования, найти производные следующих функций.
Пример 4. 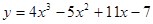 .
.
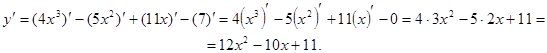
Пример 5. 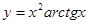 .
.
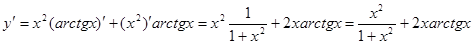 .
.
Пример 6. 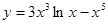 .
.
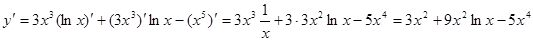 .
.
Пример 7. 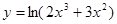 .
.
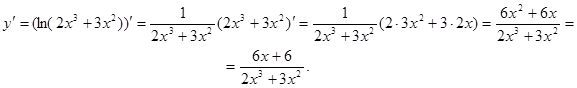
Пример 8. 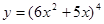 .
.
Обозначим 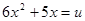 , тогда
, тогда 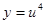 . По правилу дифференцирования сложной функции имеем
. По правилу дифференцирования сложной функции имеем
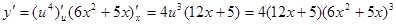 .
.
Пример 9. 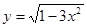 .
.
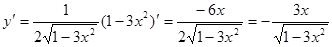 .
.
Пример 10. 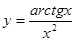 .
.
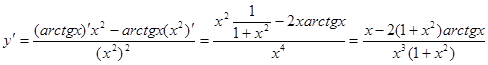 .
.
Пример 11. 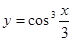 .
.
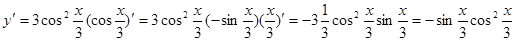 .
.
Пример 12. 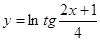 .
.
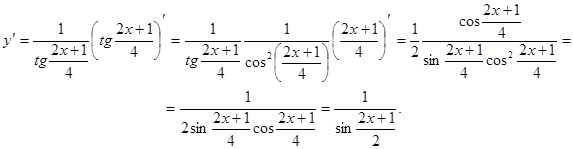
Пример 13. 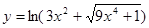 .
.
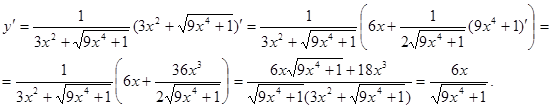
Пример 14. 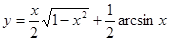 .
.
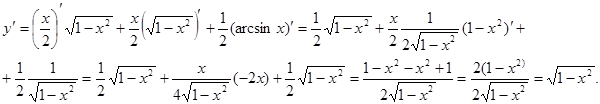
Пример 15. 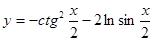 .
.
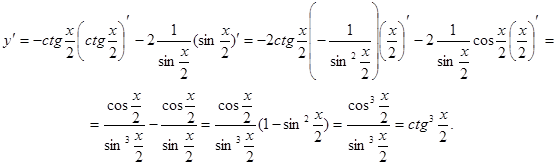
Пример 16. 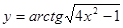 .
.
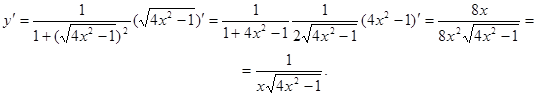
Пример 17. 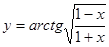 .
.
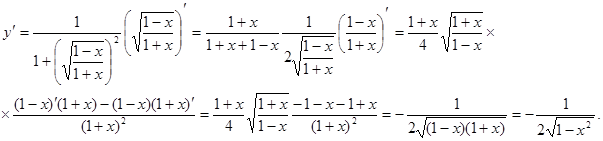
Пример 18. 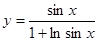 .
.
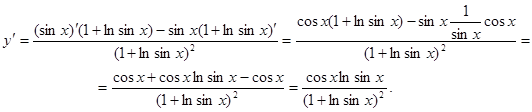
Пример 19. 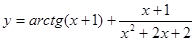 .
.
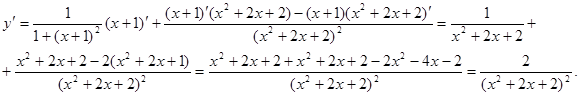
Пример 20. 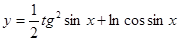 .
.
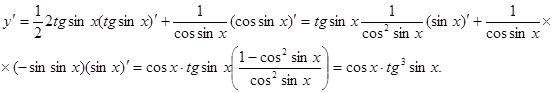
Пример 21. 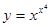 .
.
Здесь основание и показатель степени зависят от х. Логарифмируя, получим 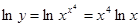 . Продифференцируем обе части последнего равенства по х. Поскольку у является функцией от х, то ln y есть сложная функция х и
. Продифференцируем обе части последнего равенства по х. Поскольку у является функцией от х, то ln y есть сложная функция х и 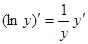 . Следовательно,
. Следовательно,
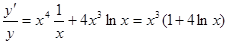 ,
,
т.е.
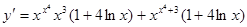 .
.
Пример 22. 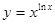 .
.
Имеем 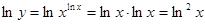 , откуда
, откуда
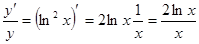 ;
;
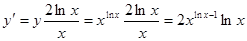 .
.
Пример 23. 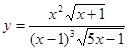 .
.
Здесь заданную функцию также следует предварительно прологарифмировать:
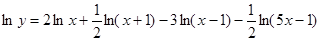 ;
;
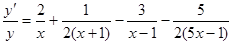 ;
;
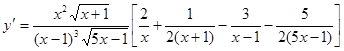 .
.
Пример 24. Составить уравнение касательной и нормали к кривой 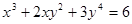 в точке М(2; -1).
в точке М(2; -1).
Из уравнения кривой найдем производную:
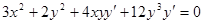 ,
,
т.е.
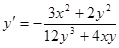 .
.
Следовательно, 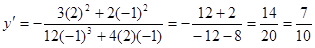 .
.
Уравнение касательной
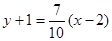 , или
, или 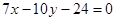 .
.
Уравнение нормали
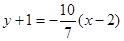 , или
, или 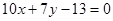 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|