Конспект урока Прямоугольный параллелепипед

Конспект урока "Прямоугольный параллелепипед"

Материал урока.

Прежде чем приступить к изучению нового материала, давайте вспомним, какую фигуру мы назвали параллелепипедом, основные свойства параллелепипеда.

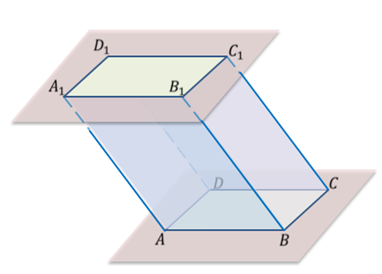
Напомним, что параллелепипедом мы назвали поверхность, составленную из двух равных параллелограммов ABCD и A₁B₁C₁D₁ и четырех параллелограммов ABB₁A₁, BCC1B₁, CDD₁C₁, DAA₁D₁.

Повторим свойства параллелепипеда. Противоположные грани параллелепипеда параллельны и равны. Например, в параллелепипеде, который показан на рисунке грань ABCD равна и параллельна грани A₁B₁C₁D₁, грань AA₁B₁B равна и параллельна грани DD₁C₁D, грань AA₁D₁D равна и параллельна грани BB₁C₁C.

Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

Эти свойства мы уже доказывали.

Когда мы изучали тему «Параллелепипед», мы говорили, что, если все боковые ребра параллелепипеда перпендикулярны к плоскостям его оснований, т. е. боковые грани – прямоугольники, то такой параллелепипед называется прямым. Если же и основаниями прямого параллелепипеда служат прямоугольники, то такой параллелепипед называется прямоугольным.

Сегодня на уроке мы познакомимся с прямоугольным параллелепипедом поближе.

Форму прямоугольного параллелепипеда имеют многие предметы.

Давайте посмотрим на рисунок.

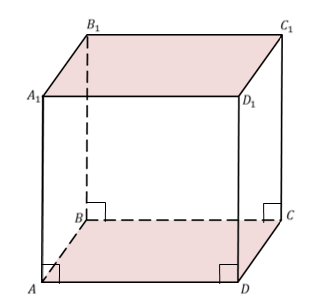
Основаниями этого прямоугольного параллелепипеда служат прямоугольники ABCD и A₁B₁C₁D₁, боковые рёбра AA₁, BB₁, CC₁, DD₁ перпендикулярны к основаниям. То есть можно записать, что AA₁ перпендикулярно AB, то есть боковая грань AA₁B₁B – прямоугольник. Аналогично, можно показать, что все боковые грани прямоугольного параллелепипеда являются прямоугольниками. Таким образом, мы обосновали свойство прямоугольного параллелепипеда.

Сформулируем его. В прямоугольном параллелепипеде все шесть граней – прямоугольники.

Полуплоскости, в которых расположены смежные грани параллелепипеда, образуют двугранные углы, которые называются двугранными углами параллелепипеда.

Рассмотрим, например, двугранный угол с ребром AB, то есть двугранный угол между плоскостями ABB₁ и ABC.

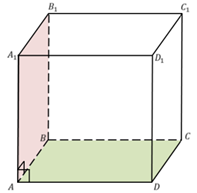
По другому этот угол можно записать так: угол A₁ABD.

Возьмем на ребре AB, например, точку А. AA₁ – перпендикуляр к ребру AB в плоскости ABB₁, АD– перпендикуляр к ребру АB в плоскости ABC. Значит, угол A₁AD – линейный угол двугранного угла. Это прямой угол, значит, двугранный угол при ребре AB – прямой.

Аналогично доказывается, что любые двугранные углы прямоугольного параллелепипеда прямые. Это утверждение является еще одним свойством прямоугольного параллелепипеда.

Длины трех ребер, имеющих общую вершину, назовем измерениями прямоугольного параллелепипеда. Например, у параллелепипеда, который изображен на рисунке в качестве измерений можно взять длины ребер AB, АD и AA₁.

Понятно, что если мы говорим, например, о размерах коробки, которая имеет форму прямоугольного параллелепипеда, то мы вместо слова измерения используем слова: длина, ширина и высота.

Давайте вспомним, что в прямоугольнике квадрат диагонали равен сумме квадратов смежных сторон. Длины смежных сторон можно назвать измерениями прямоугольника. Тогда это утверждение можно переформулировать так: квадрат диагонали прямоугольника равен сумме квадратов двух его измерений.

Аналогичным свойством обладает и прямоугольный параллелепипед.

Сформулируем теорему. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

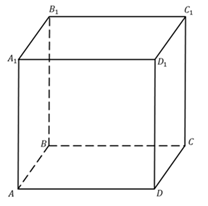
Пусть дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Тогда нам надо доказать, что, например, .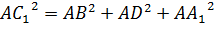

Доказательство.

Поскольку параллелепипед прямоугольный, то ребро CC₁ перпендикулярно к основанию ABCD. А, значит, угол ACC₁ – прямой.

Рассмотрим треугольник ACC₁. Это прямоугольный треугольник, значит, по теореме Пифагора можно записать, что .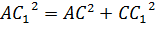

AC – диагональ прямоугольника ABCD. Значит, по свойству диагоналей прямоугольника можно записать, что . Кроме того, мы знаем, что ребро CC₁ равно AA₁. Тогда подставив все в выражение для 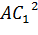, получим, что .

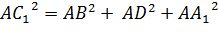Что и требовалось доказать.

Теперь давайте сформулируем и докажем следствие из этой теоремы.

Диагонали прямоугольного параллелепипеда равны.

Это следствие легко доказать, если мы посмотрим на доказательство теоремы. Мы могли взять вместо диагонали AC₁, например, диагональ CA₁ или диагонали BD₁ или DB₁, но мы бы получили то же самое выражение.

Если мы обозначим измерения прямоугольного параллелепипеда буквами a, b, c, тогда можно записать, что .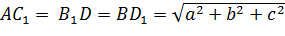

Если все измерения прямоугольного параллелепипеда равны, то такой прямоугольный параллелепипед называется кубом.

Поскольку все измерения куба равны, значит, все грани куба – квадраты.

Решим несколько задач.

Задача.Измерения прямоугольного параллелепипеда равны 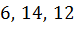. Найти длины диагоналей прямоугольного параллелепипеда.

Решение.

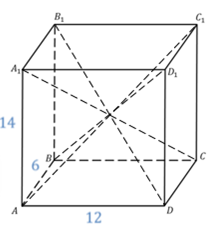
Воспользуемся следствием из теоремы и запишем, что все диагонали прямоугольного параллелепипеда равны.

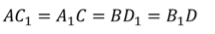
Теперь применим теорему и запишем, что диагонали равны корню квадратному из суммы квадратов измерений прямоугольного параллелепипеда.

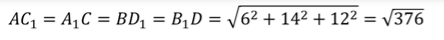
Поскольку мы знаем, что все диагонали параллелепипеда равны, при решении задач мы будем изображать только одну диагональ параллелепипеда, если условие задачи не потребует изобразить больше диагоналей.

Ответ.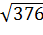

Решим еще одну задачу.

Задача.В прямоугольном параллелепипеде измерения равны 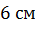, , 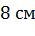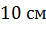. Найти диагональ параллелепипеда и синус угла между диагональю параллелепипеда и плоскостью его основания.

Решение.

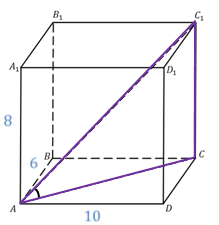
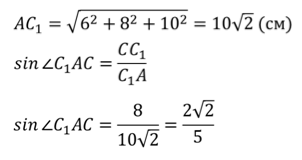
Ответ. ; .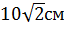

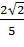А теперь давайте решим одну задачу, которую очень часто решают люди, которые делают ремонт.

Задача.Измерения комнаты равны 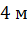, , 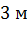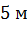. Подсчитать площадь пола, потолка, и стен комнаты.

Решение.

Каждая из граней прямоугольного параллелепипеда – прямоугольник. Для того, чтобы найти площадь каждой грани, достаточно перемножить соответствующие измерения каждого прямоугольника.

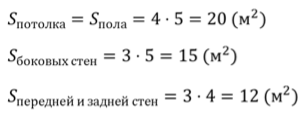
Ответ. 20м²; 15 м²; 12 м²

Решим еще одну задачу.

Задача.Диагональ прямоугольного параллелепипеда равна , а два измерения равны соответственно 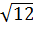и 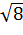. Найти третье измерение прямоугольного параллелепипеда.

Решение.

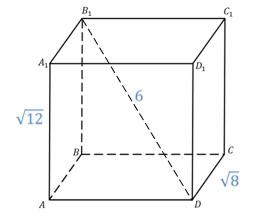
Запишем формулу, связывающую квадрат диагонали прямоугольного параллелепипеда и квадраты измерений прямоугольного параллелепипеда.

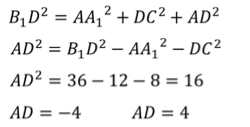
(Очевидно, что измерение прямоугольного параллелепипеда не может быть отрицательным числом).

Ответ. 4

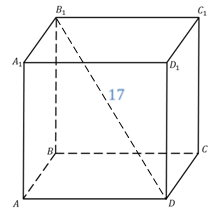
Решим еще одну задачу.

Задача.Диагональ прямоугольного параллелепипеда равна 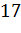, , 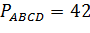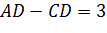. Найти третье измерение прямоугольного параллелепипеда.

Решение.

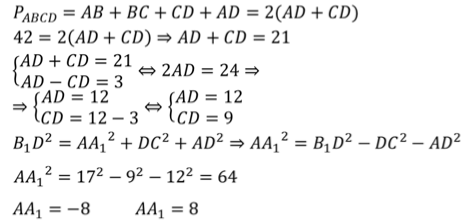
Ответ. 8

Решим еще одну задачу.

Задача.Измерения параллелепипеда равны , , 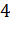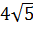. На ребре 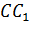прямоугольного параллелепипеда, изображенного на рисунке, дана точка 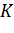такая, что отношение 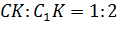. На ребре 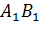отмечена точка 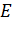так, что 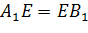. На отрезке 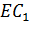отмечена точка 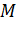, которая является серединой отрезка 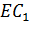. Найти длину отрезка .

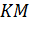Решение.

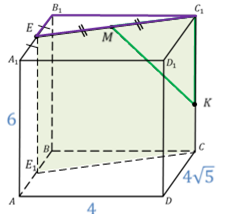
Сначала построим плоскость, в которой будет лежать отрезок МК. Для этого достаточно из точки Е опустить перпендикуляр на грань ABCD. Получим точку E₁. Тогда в плоскости EE₁C и будет лежать искомый отрезок КМ.

Найдем длину отрезка KC₁.Рассмотрим треугольник EB₁C₁.

Теперь из треугольника MKC₁ определим МК.