
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Контрольная работа
Министерство образования и науки Российской Федерации
ФГАОУ ВО «УрФУ имени первого Президента России Б.Н. Ельцина»
Институт новых материалов и технологий
Кафедра «Металлургия железа и сплавов»
Оценка работы______________
Руководитель от УрФУ_________/Спирин Н.А.
Контрольная работа
1. На тему: «Использование статистических гипотез для проверки гипотез о виде функции распределения»
Студент А.С. Тренин
Подпись ФИО
Группа НМТЗМ-102203
Екатеринбург 2021
Рассмотренные ранее методы оценивания параметров распределения случайной величины и критерии для проверки статистических гипотез предполагали, что известна функция распределения (нормальный закон – распределение Гаусса). Однако в большинстве случаев вид закона распределения является гипотетическим и сам по себе требует статистического подтверждени.
Разработано достаточно много критериев согласия, отличающихся как своей мощностью, так и объемом опытных данных, необходимых для их использования. Рассмотрим некоторые из них, и в первую очередь остановимся на критериях согласия, которые могут быть использованы при относительно больших объемах выборки.
Когда экспериментатор располагает достаточно представительным количеством экспериментальных данных (n > 100), то их предварительная обработка начинается с группировки, которая проводится в следующей последовательности:
1. Находят наибольшее (x max) и наименьшее (x min) выборочные значения случайной величины и вычисляют ее размах R= x max-x min.
2. Размах случайной величины разбивают на k равных интервалов. Количество интервалов k выбирают в зависимости от объема выборки. Например, при n >100 его значение рекомендуется принимать равным k=9¸15 (при n <100 k=7). Число интервалов k можно определить и по формуле Штюргеса k=1+3,32lg(n) с округлением полученного значения до ближайшей целой величины.
3. Определяют ширину интервала h=R/k, для упрощения расчетов полученные значения округляют в любую сторону, несколько увеличивая или уменьшая при этом размах варьирования R.
4. Устанавливают границы интервалов и подсчитывают число попаданий случайной величины в каждый из выбранных интервалов
5. Определяют частоту попаданий для каждого интервала как Pi=/n. Результаты подобных вычислений могут быть сведены в таблицу
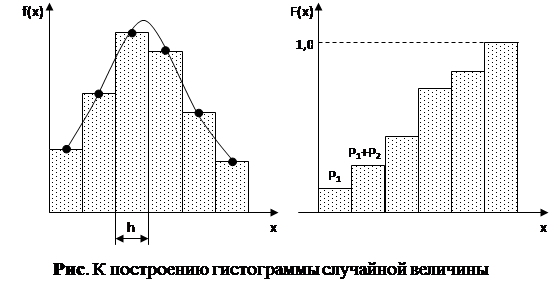
Графической формой представления непрерывной случайной величины является гистограмма (рис.). Последовательность построения гистограмм следующая:
1. Определяется величина кординаты 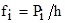 , где Pi – вероятность появления случайной величины в i-м интервале.
, где Pi – вероятность появления случайной величины в i-м интервале.
2. В системе координат fi=f(x) на ширине интервала h откладывают величины fi как высоты и строятся прямоугольники.
Очевидно, что площадь элементарного прямоугольника
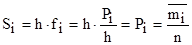
равна отношению числа опытов mi, при которых случайная величина оказалась внутри этого интервала, к общему числу опытов n.
Площадь всей гистограммы 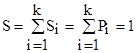 . Следовательно, площадь, ограниченная гистограммой, равна единице.
. Следовательно, площадь, ограниченная гистограммой, равна единице.
3. Построение гистограммы интегральной функции распределения осуществляется суммированием вероятностей: 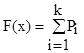 .
.
В дальнейшем осуществляется сравнение экспериментально полученного распределения случайной величины с некоторым видом теоретического распределения. Для этой цели используются различные критерии согласия: c2 (хи-квадрат) Пирсона, Колмогорова–Смирнова
Критерий Пирсона
Рассмотрим методику проверки гипотезы нормального распределения по критерию c2 Пирсона. Этот критерий кроме определения доверительного интервала для дисперсии нередко используется для проверки согласованности
распределений, полученных по данным выборки с некоторой теоретической плотностью распределения.
В данном случае применение критерия c2 предполагает использование свойств нормированного (стандартного) нормального распределения. Напомним, что уравнение кривой плотности стандартного нормального распределения имеет вид
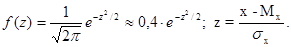
Тогда теоретическая вероятность попадания случайной величины в интервал Dz=zi+1 – zi в случае нормального распределения можно определить по формуле
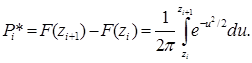 (3.54)
(3.54)
Отличие оценки закона распределения P от теоретического закона распределения P* можно охарактеризовать величиной
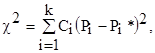 (3.55)
(3.55)
где Pi и Pi* – оценка и теоретическая вероятность случайной величины для i-го интервала; Ci – весовые коэффициенты, которые с большим весом учитывают отклонения для меньших Pi.
Пирсон выбрал весовые коэффициенты следующим образом:
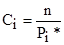 . (3.56)
. (3.56)
Пирсон показал, что при таком выборе Ci закон распределения c2 слабо зависит от n и P(x), а определяется в основном числом разрядов k.
Следовательно,
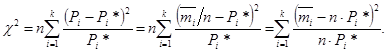 (3.57)
(3.57)
Очевидно, что при идеальном соответствии экспериментальных данных нормальному закону распределения экспериментальное значение критерия Пирсона будет равно нулю, т.к. Pi= Pi*.
В выражении (3.55) стоит сумма квадратов k случайных величин, однако они не являются независимыми, так как на них накладывается некоторое число связей. Одной из таких связей является требование, чтобы площадь под кривой оценки закона распределения равнялась единице: 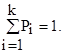 Иногда требуют, чтобы среднее значение
Иногда требуют, чтобы среднее значение 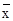 совпадало с математическим ожиданием Mx, а выборочная дисперсия Sx2 – с дисперсией sx2. Поэтому число степеней свободы чаще всего определяется как
совпадало с математическим ожиданием Mx, а выборочная дисперсия Sx2 – с дисперсией sx2. Поэтому число степеней свободы чаще всего определяется как
m = k - 2. (3.58)
Теоретическое значение критерия Пирсона c2a;m определяется по справочным данным (см. табл.П.3) или с использованием пакетов прикладных программ при заданном уровне значимости a и числе степеней свободы m (см. функцию ХИ2.ОБР.ПХ(a;m) из электронных таблиц Microsoft Excel).
Алгоритм использования критерия Пирсона заключается в следующем.
1. Выдвигаются нуль-гипотеза Н0: "Отличие экспериментальных данных от нормального закона распределения не существенно" и альтернативная ей гипотеза Н1: "Отличие экспериментальных данных от нормального закона распределения существенно, т.е. экспериментальные данные не подчиняются закону нормального распределения".
2. По результатам экспериментальных измерений и предположению нормального закона их распределения определяется расчетное значение критерия Пирсона c2.
3. Определяют число степеней свободы m, задаются уровнем значимости a и определяют теоретическое значение критерия Пирсона c2µ;m.
4. Если c2<c2µ;m, то нуль-гипотеза Н0 о нормальном законе распределения экспериментальных данных принимается с доверительной вероятностью P=1-a. В противном случае нуль-гипотеза отвергается и принимается альтернативная гипотеза Н1.
Отметим важные рекомендации по использованию критерия c2.
Если при некотором числе измерений критерий c2 >c2µ;m, но сомнения в нормальности распределения отсутствуют, то следует, если имеется возможность, увеличить число измерений в несколько раз и повторить анализ по этому же критерию.
Число степеней свободы m=k-2 относится к такому случаю, когда оба параметра нормального закона распределения определяются по результатам измерений, т.е. когда вместо точных измерений значений Mx и sx применяют их эмпирические значения (оценки) 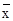 и Sx. Если же значение Mx точно известно (например, при измерении эталона), то число степеней свободы равно k=n-1; если известны оба параметра Mx и sx, то число степеней свободы равно k=n. На практике такая ситуация встречается относительно редко, и поэтому для получения числа степеней свободы не менее пяти желательно брать число интервалов не менее семи (иногда девяти).
и Sx. Если же значение Mx точно известно (например, при измерении эталона), то число степеней свободы равно k=n-1; если известны оба параметра Mx и sx, то число степеней свободы равно k=n. На практике такая ситуация встречается относительно редко, и поэтому для получения числа степеней свободы не менее пяти желательно брать число интервалов не менее семи (иногда девяти).
Критерий Колмогорова–Смирнова
Рассмотрим использование критерия Колмогорова–Смирнова для проверки гипотезы нормальности распределения случайных величин. Данная процедура также предполагает построение таблицы распределения экспериментально полученных значений с группировкой данных в определенное число разрядов k. Дополнительно в таблицу необходимо включить следующие колонки:
колонку с накопительной суммой 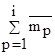 для каждого i-го интервала сгруппированных данных
для каждого i-го интервала сгруппированных данных
Процедура вычисления критерия Колмогорова–Смирнова
| Интервал | Число замеров
в каждом
интервале 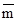 i i
| 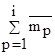
| Теоретичес-кая вероятность Pi* | 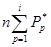
| 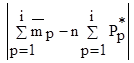
|
| x1 ¸ x2 | 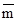 1 1
| 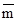 1 1
| P1* | 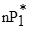
| ½ 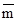 1- 1- 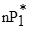 ½ ½
|
| x2 ¸ x3 | 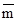 2 2
| 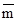 1+ 1+ 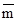 2 2
| P2* | n( 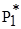 + + 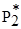 ) )
| ½ ( 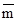 1+ 1+ 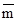 2)-
-n( 2)-
-n( 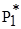 + + 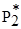 )½ )½
|
| ... | ... | … | … | … | … |
| xi ¸ xi+1 | 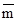 i i
| 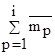
| Pi* | 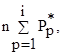
| 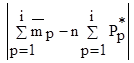
|
| ... | ... | … | … | … | … |
| xk ¸ xk+1 | 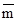 k k
| 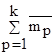
| Pk* | 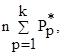
| 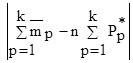
|
колонку с накопительной суммой 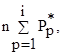 где Р* – теоретическ
где Р* – теоретическ
Далее экспериментальное значение критерия Колмогорова–Смирнова сравнивают с теоретическим Dn;a, которое определяют из статистических таблиц в соответствии с объемом выборки n и требуемым уровнем значимости a (см. табл. П.10). Если D<Dn;a , то гипотеза о нормальном распределении результатов замеров принимается с вероятностью P=1-a.
Критерий согласия Колмогорова–Смирнова для проверки нормальности распределения результатов наблюдений входит в пакет статистической обработки данных STATISTICA, с которым мы познакомимся в главе 7.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|