Аксиоматическое определение множества действительных чисел: аксиомы сложения, умножения, порядка, понятия о натуральных, целых и рациональных числах.

БИЛЕТ 1

1.Аксиоматическое определение множества действительных чисел: аксиомы сложения, умножения, порядка, понятия о натуральных, целых и рациональных числах.

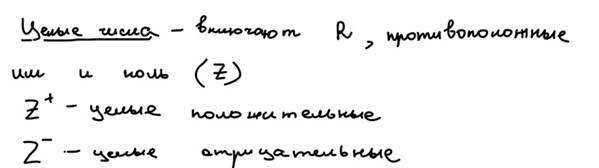
Рациональное число - это число, представимое в виде обыкновенной дроби p делить на q, где p - целое, а q – натуральное.

Предел функции в точке (различные определения) его геометрический смысл, примеры.

1. Предел функции

Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Определение ПО КОШИ. Число b называется пределом функции f в точке x=a, если для любого числа ε>0, сколь малым оно бы ни было, существует положительное число δ такое, что для всякого x, удовлетворяющего условию 0<|x−a|<δ, выполняется неравенство |f(x)−b|<ε. Другими словами, число b называется пределом функции f в точке x = a, если ∀ε>0 ∃δ>0: ∀x, 0<|x−a|<δ, |f(x)−b|<ε. Это определение называется определением предела функции по Коши, или на языке ε-δ.

Определение ПО ГЕЙНЕ.Число b называется пределом функции f в точке x=a (или при x → a), если для любой последовательности {x_n}, сходящейся к a и такой, что x_n ̸=a для всех n ∈ N, соответствующая последовательность значений функции {f(x_n)} сходится к b. Другими словами, число b называется пределом функции f в точке x=a, если ∀{x_n}, x_n ̸=a (n∈N), .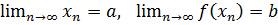

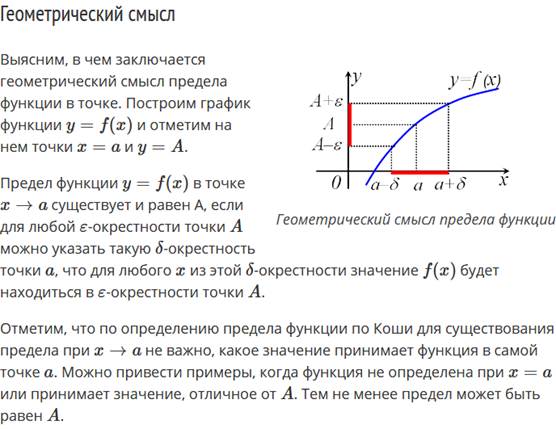
Определение(ЯЗЫК ОКРЕСТНОСТЕЙ) Число b называется пределом функции f в точке x = a, если для любой ε-окрестности точки b найдется такая δ-окрестность точки a, что для всех x ̸= a из этой δ-окрестности соответствующие значения функции f(x) лежат в ε-окрестности точки b. Это определение называется определением предела функции на языке окрестностей и выражает геометрический смысл предела функции.