
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа № 8. Изучение синтеза логических схем в различных базисах. Теоретический материал. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
Практическая работа № 8
Изучение синтеза логических схем в различных базисах
Теоретический материал
ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
Логический элемент в электронных схемах – это устройство, реализующее ту или иную логическую функцию. При этом логические сигналы 0 и 1 задаются разными уровнями напряжения. Сигнал логического нуля обычно представляется низким уровнем напряжения U0 , логической единицы – высоким U1 . Такая логика получила название положительной. В ряде случаев используют отрицательную логику, где логический нуль представляется высоким уровнем напряжения, а логическая единица – низким. Логические схемы состоят из логических элементов, осуществляющих логические операции.
Логические схемы реализуются на логических элементах: "НЕ", "И", "ИЛИ", "И-НЕ", "ИЛИ-НЕ", "Исключающее ИЛИ" и "Эквивалентность".
Три приведенных ниже логических элемента составляют функционально полную систему для проектирования цифровых логических устройств, в том числе и соответствующих логических блоков и устройств компьютера, поскольку реализуют функционально полный набор логических функций, состоящий из логических функций: И (конъюнкции), ИЛИ (дизъюнкции), НЕ (отрицания).
1. Логический элемент НЕ, который называется также инвертором, выполняет логическую операцию отрицания (инверсии).

2. Логический элемент И, называемый также конъюнктором, выполняет операцию логического умножения (конъюнкции), теоретически может иметь бесконечное число входов, на практике ограничиваются числом входов от двух до восьми.

3. Логический элемент ИЛИ, называемый также дизъюнктором, выполняет операцию логического сложения (дизъюнкции), теоретически может иметь бесконечное число входов, на практике ограничиваются числом входов от двух до восьми.
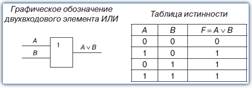
При проектировании цифровых логических устройств часто возникает задача по заданной таблице истинности записать выражение для логической функции и реализовать ее в виде логической схемы, состоящей из функционально полного набора логических элементов. Данную задачу называют также задачей синтеза логических схем или логических устройств.
Синтез логических схем на основе функционально полного набора логических элементов состоит из представления логических функций, описывающих данные логические схемы в нормальных формах. Нормальной формой представления считается форма, полученная посредством суперпозиций вспомогательных логических функций – минтермов и макстернов.
При построении логической схемы необходимо учитывать установленные в алгебре логики правила (приоритеты) для выполнения логических операций.
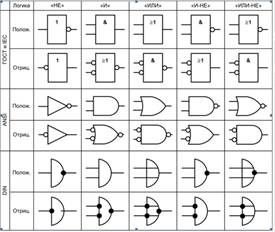
Для обозначения логических элементов используется несколько стандартов. Наиболее распространёнными являются американский (ANSI), европейский (DIN), международный (IEC) и российский (ГОСТ).
Контрольные вопросы:
1. Что такое СДНФ?
2. Что такое СКНФ?
3. Как записать СДНФ, используя таблицу истинности устройства?
4. Как записать СКНФ, используя таблицу истинности устройства?
5. Как разработать схему логического устройства, используя СДНФ?
6. Что такое минимизация логического выражения?
Задания
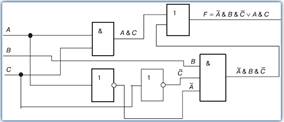
Задание 1. Найдите булеву функцию логической схемы и составьте таблицу истинности
Варианты 1,5,8,12,15,19 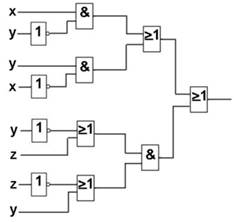
Варианты 2,3,9,10,13,18 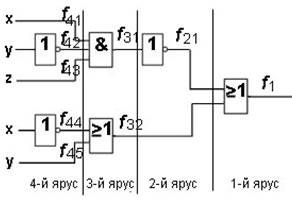
Варианты 4,6,7,11,14,16,17 
Задание 2
Для данной таблицы истинности записать СДНФ, провести минимизацию и, используя основные логические элементы – НЕ, И и ИЛИ, разработать логическую схему реализации выходной функции F.
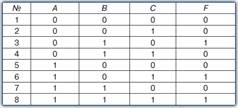
Задание 3
Построить логическую схему, реализующую функцию с данной таблицей истинности (№ функции соответствует № варианта):
| Х1 | ||||||||||||||||
| Х2 | ||||||||||||||||
| Х3 | ||||||||||||||||
| Х4 | ||||||||||||||||
| F1(Х1, Х2 ,Х3,Х4) | ||||||||||||||||
| F2(Х1, Х2 ,Х3,Х4) | ||||||||||||||||
| F3(Х1, Х2 ,Х3,Х4) | ||||||||||||||||
| F4(Х1, Х2 ,Х3,Х4) | ||||||||||||||||
| F5(Х1, Х2 ,Х3,Х4) | ||||||||||||||||
| F6(Х1, Х2 ,Х3,Х4) | ||||||||||||||||
| F7(Х1, Х2 ,Х3,Х4) | ||||||||||||||||
| F8(Х1, Х2 ,Х3,Х4) | ||||||||||||||||
| F9(Х1, Х2 ,Х3,Х4) | ||||||||||||||||
| F10(Х1, Х2 ,Х3,Х4) | ||||||||||||||||
| F11(Х1, Х2 ,Х3,Х4) | ||||||||||||||||
| F12(Х1, Х2 ,Х3,Х4) | ||||||||||||||||
| F13(Х1, Х2 ,Х3,Х4) |
Задание 1
1 2



Задание 2
СДНФ 
МДНФ 
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|