
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Исследование ВЫНУЖДЕННЫХ КОЛЕБАНИЙ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ
Исследование ВЫНУЖДЕННЫХ КОЛЕБАНИЙ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ
ЦЕЛЬ РАБОТЫ:исследовать зависимость напряжения на конденсаторе от частоты вынуждающего воздействия; определить основные параметры контура.
приборы и ПРИНАДЛЕЖНОСТИ:генератор синусоидальных сигналов, осциллограф, макет для сборки исследуемого колебательного контура (конденсатор, катушка индуктивности).
КРАТКАЯ ТЕОРИЯ
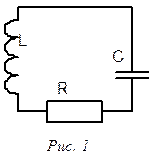 Замкнутая цепь, состоящая из емкости C, индуктивности L, активного сопротивления R, образует колебательный контур (рис. 1). Если в колебательный контур включить источник периодической (гармонической) ЭДС, то в контуре после затухания собственных колебаний установятся вынужденные электрические колебания с частотой, которая совпадает с частотой вынуждающей ЭДС. Интенсивность установившихся электрических колебаний в контуре может быть охарактеризована амплитудой тока (напряжения) на конденсаторе или индуктивности.
Замкнутая цепь, состоящая из емкости C, индуктивности L, активного сопротивления R, образует колебательный контур (рис. 1). Если в колебательный контур включить источник периодической (гармонической) ЭДС, то в контуре после затухания собственных колебаний установятся вынужденные электрические колебания с частотой, которая совпадает с частотой вынуждающей ЭДС. Интенсивность установившихся электрических колебаний в контуре может быть охарактеризована амплитудой тока (напряжения) на конденсаторе или индуктивности.
Амплитуда каждой из этих величин зависит от частоты вынуждающей ЭДС и имеет характерный максимум вблизи собственной частоты контура w0, т.е наблюдается явление резонанса. Явление резонанса состоит в резком возрастании амплитуды установившихся колебаний при приближении частоты внешней ЭДС w к собственной частоте w0 данного контура.
Поведение контура зависит от способа включения источника. Если источник включается последовательно с элементами L, C, R (рис. 2,а), то говорят о резонансе в последовательном контуре или резонансе напряжения.
Если источник ЭДС питает параллельно включенные ветви контура с L и С (рис. 2,б), то говорят о резонансе в параллельном контуре или резонансе токов. В данной работе экспериментально исследуются зависимость амплитуды Uсм переменного напряжения на конденсаторе от частоты напряжения последовательно включенного источника.
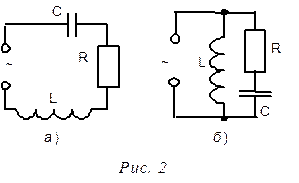
Уравнение амплитудной резонансной кривой Uсм=f(w) может быть получено следующим образом.
Приравняв сумму падений напряжения на элементах контура к приложенному напряжению (второе правило Кирхгофа):
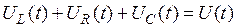 , ,
|
где
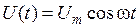 , ,
|
получим уравнение вынужденных электрических колебаний:
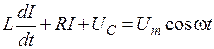 . .
| (1) |
Произведя преобразования, получим уравнение
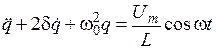 . .
|
где 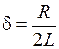 - коэффициент затухания;
- коэффициент затухания; 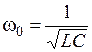 - собственная частота контура.
- собственная частота контура.
Учитывая, что
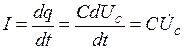 , (q=CUC), , (q=CUC),
|
получим
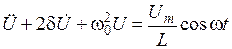 . .
| (2) |
Частное решение уравнения (2) (для установившегося режима) имеет вид:
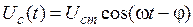 , ,
|
где 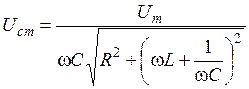 является аналитическим выражением амплитудной резонансной кривой для напряжений на конденсаторе;
является аналитическим выражением амплитудной резонансной кривой для напряжений на конденсаторе;
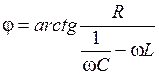 – сдвиг фаз между внешним напряжением и напряжением на конденсаторе.
– сдвиг фаз между внешним напряжением и напряжением на конденсаторе.
Нетрудно показать, что амплитуда напряжения на конденсаторе достигает максимума при частоте 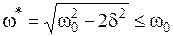 . Типичные амплитудные резонансные кривые Ucm=f(w) (амплитудно-частотная характеристика) для различных значений активного сопротивления контура представлены на рис. 3.
. Типичные амплитудные резонансные кривые Ucm=f(w) (амплитудно-частотная характеристика) для различных значений активного сопротивления контура представлены на рис. 3.
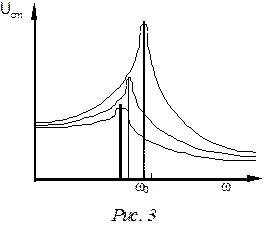
Известно, что часто свойства колебательной системы удобно характеризовать добротностью Q, которая определяется как величина, обратно пропорциональная логарифмическому декременту затухания 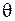 :
:
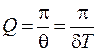 , или
, или 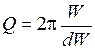 ,
,
где W - энергия, запасенная в контуре;
dW - уменьшение энергии контура за период.
Последняя формула наиболее отчетливо отражает физический смысл добротности. Если затухание невелико ( 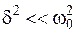 ), то теоретическое значение добротности может быть рассчитано по формуле:
), то теоретическое значение добротности может быть рассчитано по формуле:
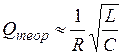 . .
| (3) |
Добротность контура можно легко определить из данных исследования явления резонанса. При малом затухании
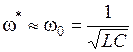 . .
| (4) |
Тогда 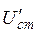 при резонансе будет равно
при резонансе будет равно
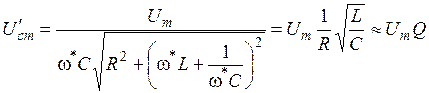 .
.
Отсюда экспериментальное значение добротности контура можно также определить как отношение максимальной амплитуды напряжения на конденсаторе к амплитуде включенного напряжения:
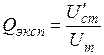 . .
| (5) |
Значение напряжения в максимуме (амплитуды) Ucm является одной из характеристик амплитудной резонансной кривой. Другой важной характеристикой является ширина резонансной кривой Dw (полоса пропускания контура). Ширина резонансной кривой определяется как интервал частот, на котором амплитуда напряжения (тока) не бывает меньше определенного значения. Пусть w1 и w2 - значения частот, при которых энергия колебаний вдвое меньше энергии в максимуме. Тогда, учитывая, что 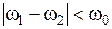 и
и 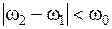 , можно показать, что:
, можно показать, что:
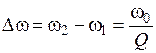 .
.
Отсюда видно, что чем больше добротность контура, тем уже резонансная кривая. Далее из формул получаем:
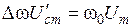 .
.
Таким образом видно, что чем больше максимум резонансной кривой, тем он острее, т.е. тем уже резонансная кривая (рис. 3).
Итак, максимум при резонансе получается тем выше и острее, чем меньше коэффициент затухания, т.е. чем меньше активное сопротивление и больше активность контура (рис. 4).
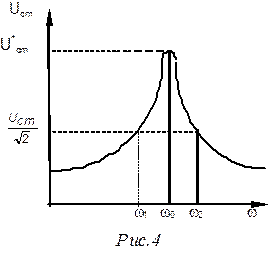
Резонансная частота wрез для любого контура определяется из условия, что сдвиг фаз тока и напряжения близок к нулю (реактивное сопротивление контура равно нулю), и тем самым создаются наилучшие условия для передачи энергии от генератора к контуру. Из этого условия получаем, что резонансная частота контура wрез при резонансе напряжения равна собственной частоте w0:
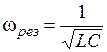 .
.
Амплитуда напряжения на конденсаторе при резонансе напряжения достигает максимального значения 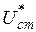 при частоте
при частоте 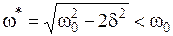 , всегда чуть меньшей резонансной частоты. Однако, если учесть, что резонанс имеет место при
, всегда чуть меньшей резонансной частоты. Однако, если учесть, что резонанс имеет место при 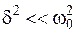 , то приблизительно:
, то приблизительно:
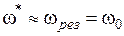 .
.
Явление резонанса напряжения широко используется для выделения из сложного напряжения нужной составляющей. Пусть, например, напряжение, приложенное к контуру, равно:
U=Um1cos(w1t+a1)+Um2cos(w2t+a2).
Настроив контур на одну из частот wi (подобрав соответствующим образом его параметры L и С), можно получить на конденсаторе напряжение, в Q раз превышающее значение данной составляющей, в то время как напряжение, создаваемое на конденсаторе другими составляющими, будет малым. Такой процесс осуществляется, например, при настройке радиоприемника на нужную длину волны.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|