
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Интегрирование методом замены переменной
Интегрирование методом замены переменной
Пусть требуется найти интеграл  , причём непосредственно подобрать первообразную для
, причём непосредственно подобрать первообразную для  мы не можем, но нам известно, что она существует.
мы не можем, но нам известно, что она существует.
Сделаем замену переменной в подынтегральном выражении, положив
 ,
,
где  - непрерывная функция с непрерывной производной, имеющая обратную функцию. Тогда
- непрерывная функция с непрерывной производной, имеющая обратную функцию. Тогда  и имеет место равенство:
и имеет место равенство:
 . (7)
. (7)
Формула (7) называется формулой замены переменной под знаком неопределённого интеграла.
Пример: 
Делаем замену  , тогда
, тогда  ,
,  .
.
Замечание. При интегрировании иногда целесообразно подбирать замену переменной в виде не  , а
, а  . Пусть, например, требуется вычислить интеграл
. Пусть, например, требуется вычислить интеграл 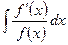 . В результате подстановки
. В результате подстановки  ,
,  получаем:
получаем:
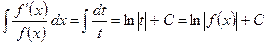 .
.
Пример: 
Замена: 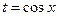 ,
, 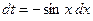 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|