
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Матрицы и действия над ними. Определители. Обратная матрица. ЛИТЕРАТУРА
4. ЗАДАЧИ И УПРАЖНЕНИЯ 
4.1 Матрицы и действия над ними
1. Найти сумму, разность, произведения двух матриц А и В.
а) 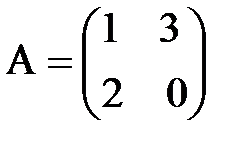 ,
, 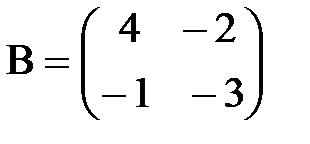 ;
;
б)  ,
, 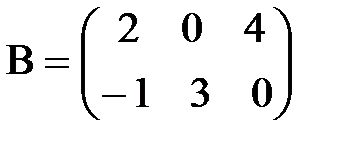 ;
;
в) 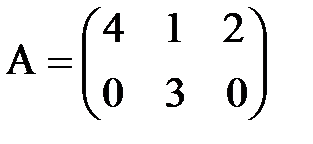 ,
, 
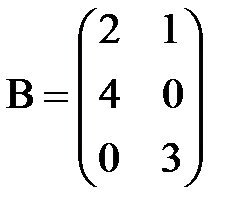 ;
;
г) 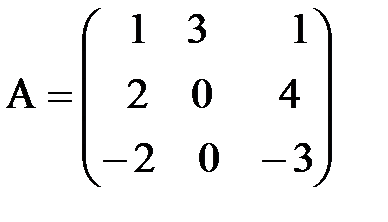 ,
, 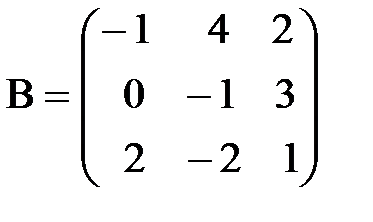 ;
;
д) 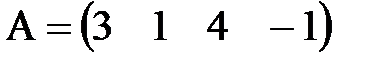 ,
, 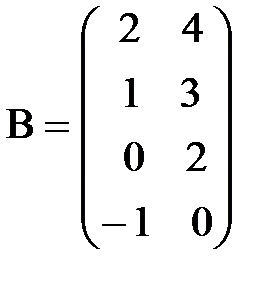 ;
;
е)  ,
,  ;
;
ж) 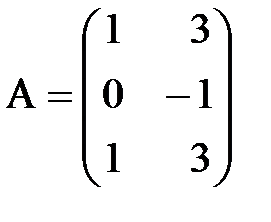 ,
, 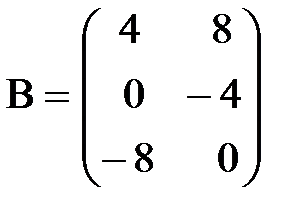 ;
;
з) 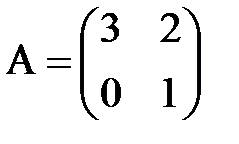 ,
,  ;
;
и)  ,
,  .
.
2. Доказать, что матрицы А и В коммутирующие.
а)  ,
, 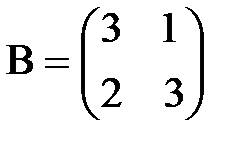 ; б)
; б) 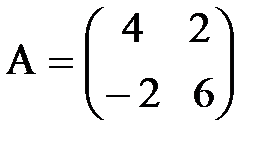 ,
, 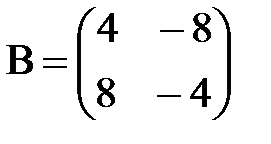 .
.
3. Даны матрицы А. В и С. Показать, что (АВ)·С=А·(ВС).
а) 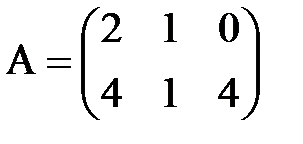 ,
, 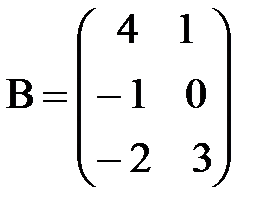 ,
, 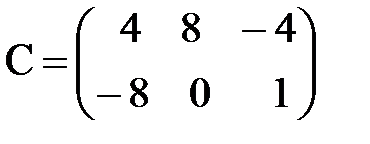 ;
;
б)  ,
, 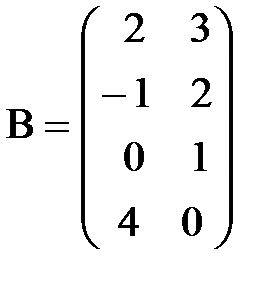 ,
, 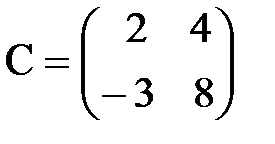 .
.
4. Вычислить (3А – 2В)·С, если
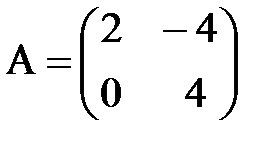 ,
, 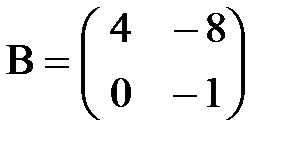 ,
, 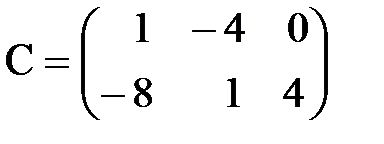 .
.
5. Найти 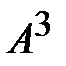 , если
, если
а) 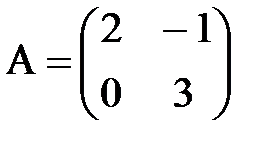 ; б)
; б) 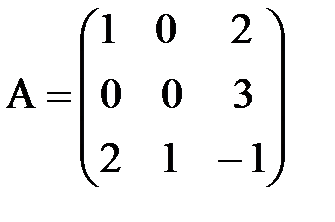 .
.
6. Найти матрицу Х, если 3А+2Х=В, где
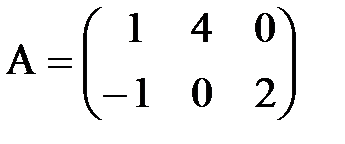 ,
, 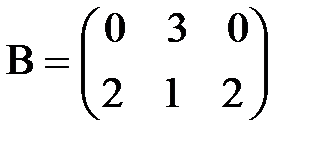 .
.
7. Найти АВС, если
а) 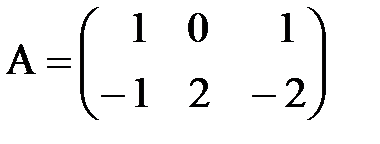 ,
,  ,
,  ;
;
б) 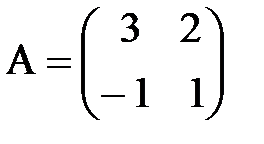 ,
, 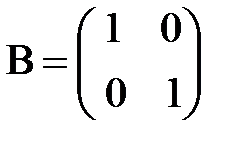 ,
, 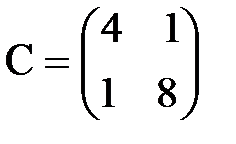 .
.
4.2 Определители
1. Вычислить определители
2.
а) 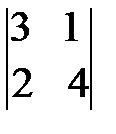 ; б)
; б) 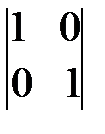 ; в)
; в) 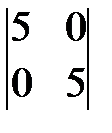 ; г)
; г) 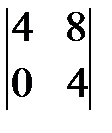 ; д)
; д) 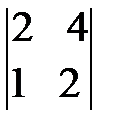 ; е)
; е) 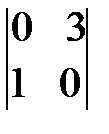 ;
;
ж) 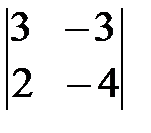 ; з)
; з)  .
.
3. С помощью правила треугольников вычислить определители
а)  ; б)
; б) 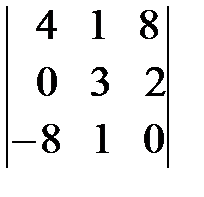 ; в)
; в) 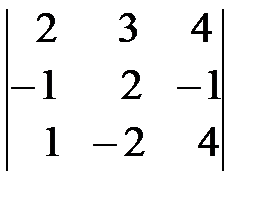 ; г)
; г) 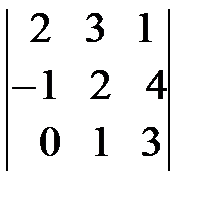 .
.
4. Вычислить определители примера 2, используя теорему Лапласа.
5. Вычислить определители, предварительно упростив их:
а)  ; б)
; б) 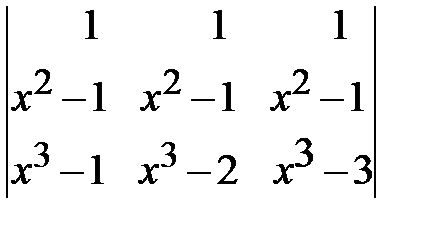 ; в)
; в)  ;
;
г) 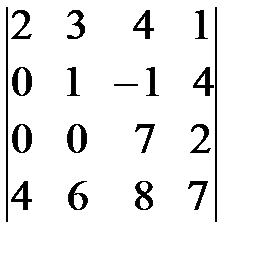 ; д)
; д) 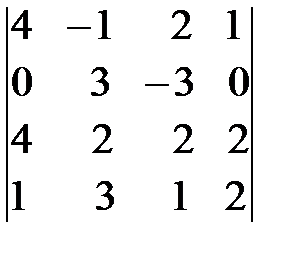 ; е)
; е) 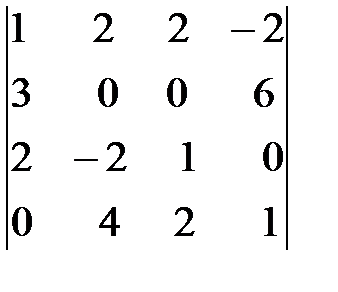 ;
;
ж)  .
.
6. Вычислить определитель методом приведения его к треугольному виду
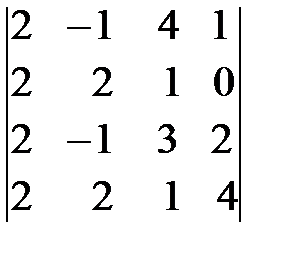 .
.
7. Пусть даны матрицы А и В. Доказать, что 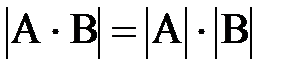 :
:
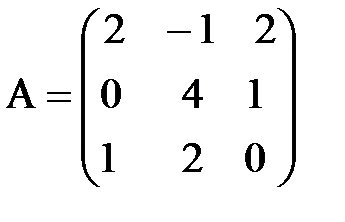 ,
, 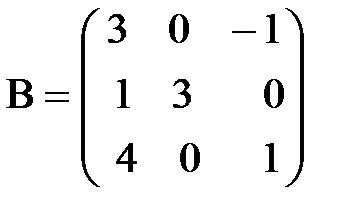 .
.
4.3 Обратная матрица
1. Найти обратную матрицу:
а)  ; б)
; б) 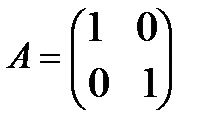 ; в)
; в) 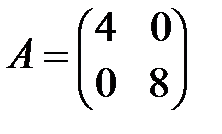 ; г)
; г) 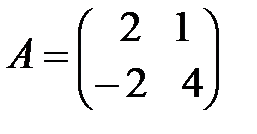 ;
;
д) 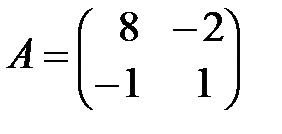 ; е)
; е) 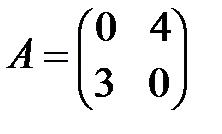 ; ж)
; ж) 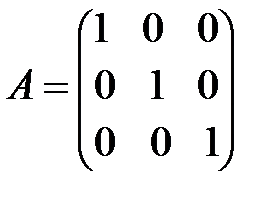 ; з)
; з) 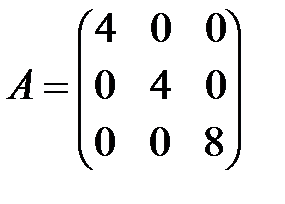 ;
;
и)  ; к)
; к)  ; л)
; л) 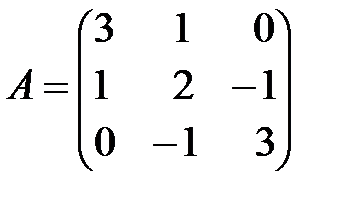 ;
;
м) 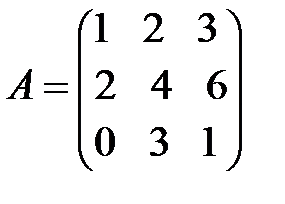 ; н)
; н) 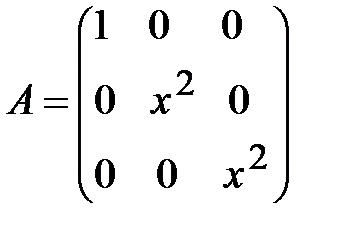 .
.
2. Найти обратную матрицу и проверить выполнение условия 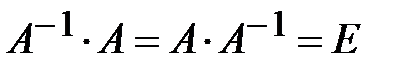 :
:
а) 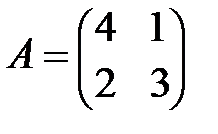 ; б)
; б) 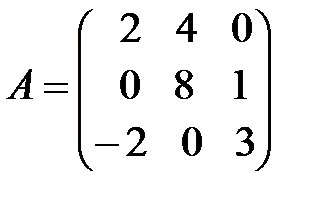 .
.
3. Доказать равенство 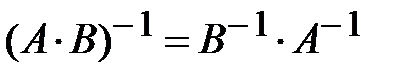 :
:
а) 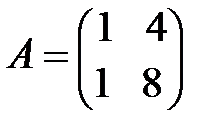 ,
, 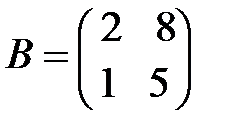 ; б)
; б) 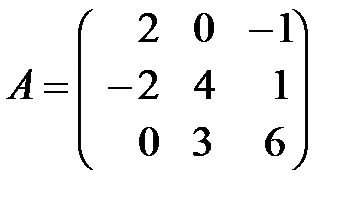 ,
, 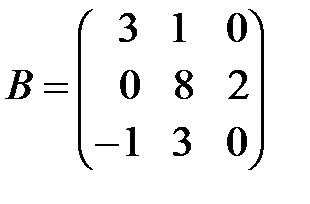 .
.
4. Доказать равенство 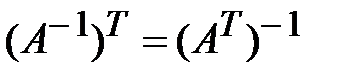 :
:
а) 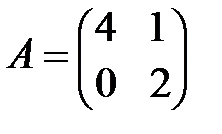 ; б)
; б) 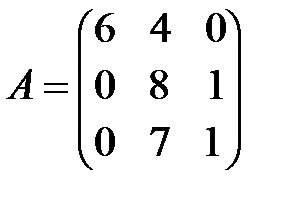 .
.
ЛИТЕРАТУРА
1. Жевняк Р.М., Карпук А.А. Высшая математика. – Мн.: Выш. шк., 1992.- 384 с.
2. Гусак А.А. Справочное пособие к решению задач: аналитическая геометрия и линейная алгебра. – Мн.: Тетрасистемс, 1998.- 288 с.
3. Марков Л.Н., Размыслович Г.П. Высшая математика. Часть 1. –Мн.: Амалфея, 1999. – 208 с.
4. Белько И.В., Кузьмич К.К. Высшая математика для экономистов. I семестр. М.: Новое знание, 2002.- 140 с.
5. Коваленко Н.С., Минченков Ю.В., Овсеец М.И. Высшая математика. Учеб. пособие. -Мн.: ЧИУП, 2003. – 32 с.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|