
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Векторное и смешанное произведение векторов
Векторное и смешанное произведение векторов
План
1. Векторное произведение векторов.
2. Смешанное произведение векторов.
3. Примеры
Вопрос 1. Векторное произведение векторов.
Векторным произведением двух векторов 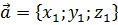 и
и 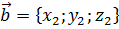 называется вектор, значение которого можно вычислить по формуле:
называется вектор, значение которого можно вычислить по формуле:
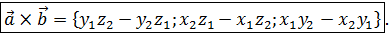
Свойства векторного произведения
1) 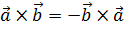
2) 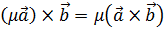 , где
, где 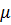 - некоторое число
- некоторое число
3) ( 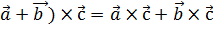
4) Длина векторного произведения двух векторов 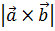 равна площади параллелограмма, построенного на приведённых к началу векторах
равна площади параллелограмма, построенного на приведённых к началу векторах 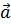 и
и 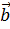 .
.
Вопрос 2. Смешанное произведение векторов
Смешанным произведением векторов 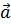 ,
, 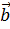 ,
, 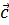 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 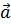 на векторное произведение векторов
на векторное произведение векторов 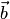 и
и 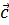
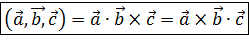
Смешанное произведение трех некомпланарных векторов геометрически равно объему параллелепипеда, построенного на этих векторах, взятому по модулю.
Вопрос 3. Примеры
Пример 1. Для векторов 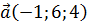 и
и 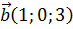 вычислим векторное произведение.
вычислим векторное произведение.
Воспользовавшись формулой, получим 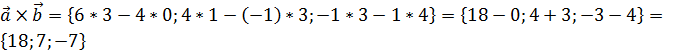 . То есть смешанное произведение заданных векторов – это вектор
. То есть смешанное произведение заданных векторов – это вектор 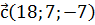 .
.
Пример 2. Вычислим смешанное произведение векторов 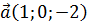 ,
, 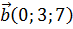 и
и 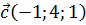 .
.
В первую очередь вычислим векторное произведение векторов 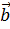 и
и 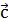 . По формуле получим
. По формуле получим 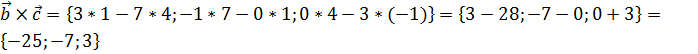 .
.
Теперь вычислим скалярно 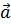 на
на 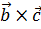 :
:
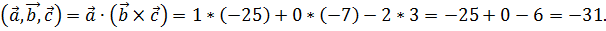
Таким образом смешанное произведение трёх заданных векторов равно -31.
Пример 3. Найдём объём параллелепипеда, построенного на векторах 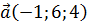 ,
, 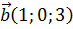 и
и 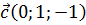 .
.
Объём такого параллелепипеда равен смешанному произведению трёх заданных векторов. Векторное произведение векторов 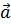 и
и 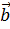 было найдено в первом примере. Осталось вычислить скалярно
было найдено в первом примере. Осталось вычислить скалярно 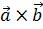 на
на 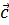 :
:
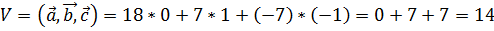 .
.
То есть объём параллелепипеда равен 14 куб.ед.
Пример 4. Найдём площадь параллелограмма, построенного на векторах 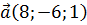 и
и 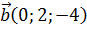 .
.
Площадь такого параллелограмма можно вычислить с помощью смешанного произведения:
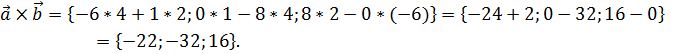
Вычислим длину полученного вектора:
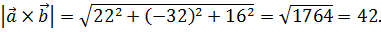
Площадь параллелограмма равна 42 кв.ед.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|