Построение графиков функций. Пример 1.

4. Построение графиков функций

График функции у=ƒ(х) часто строят «по точкам». Однако при таком способе построения можно пропустить важные особенности графика функции.

В тех случаях, когда речь идет о построении графика незнакомой функции, когда заранее невозможно представить вид графика, полезно применять определенную схему исследования свойств функции, которая помогает составить представление о её графике. Когда такое представление составится, можно приступить к построению графика по точкам.

Примерный план исследования:

1. Находят область определения функции ƒ.

2. Исследуют функцию на четность или нечетность.

3. Находят точки пересечения графика функции с осью абсцисс (для этого решают уравнение ƒ(х)=0) и с осью ординат (у = ƒ(0)).

4. Находят точки разрыва функции.

5. Точки, найденные в п. 3 и 4, разбивают ось абсцисс на несколько промежутков - это промежутки знакопостоянства функции ƒ, находят знак функции на каждом из этих промежутков.

6. Изучают поведение функции около точек разрыва и на бесконечности и находят её асимптоты.

7. Исследуют функцию на возрастание и убывание.

8. Находят точки максимума и минимума функции.

9. Исследуют график на выпуклость и находят точки перегиба.

10. Учитывая проведенное исследование, строят эскиз графика функции.

Если выполнение каких-либо шагов предложенной схемы сопряжено с техническими трудностями, их иногда можно опустить.

Пример 1.

Построим график функции, где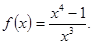

Решение:

1) Область определения D(ƒ) = (-∞; 0) U (0; +∞). Т.к. х ≠ 0.

2) Так как

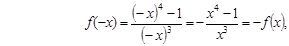то функция ƒ нечетна. Достаточно построить её график на луче (0; +∞) и отразить его симметрично относительно начала координат.

3) Найдем точки пересечения графика функции с осью Ох.

Решая уравнение = 0 находим корни 1 и –1.

Точек пересечения графика функции с осью Оу нет, т.к. х ≠ 0.

4) Т.к. х ≠ 0, то х = 0 является точкой разрыва функции.

5) Найдём промежутки знакопостоянства функции.

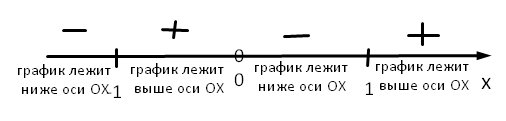
Функция ƒ положительна при х >1 и отрицательна при 0<x<1, это значит, что на промежутке (0;1) график функции лежит ниже оси абсцисс, а на промежутке (1; +∞) - выше.

6) 1.Функция определена всюду, кроме точки х = 0. В этой точке функция имеет разрыв, причём

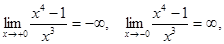значит х = 0 – вертикальная асимптота.

2. Горизонтальной асимптоты нет, так как

3. Найдём наклонную асимптоту

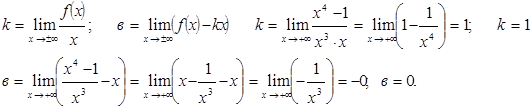
у=1∙х+0=х; у = х - наклонная асимптота.

7,8) Исследуем функцию на монотонность и найдем точки экстремума.

Имеем: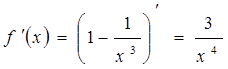

х = 0 – критическая точка, т.е. точка в которой производная не существует.

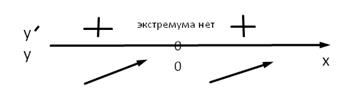
Так как при х 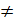0 выполнено неравенство ƒ′(х) > 0, то функция возрастает на всей области определения. Точек экстремума нет.

9) Исследуем график на выпуклость. Имеем:

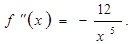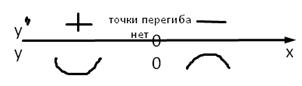
Так как при х >0 ƒ″(х) < 0, то график функции ƒ обращён выпуклостью вверх на луче (0; +∞). Так как при х < 0 ƒ″(х) > 0, то график функции ƒ обращён выпуклостью вниз на луче (-∞;0). Точек перегиба нет.

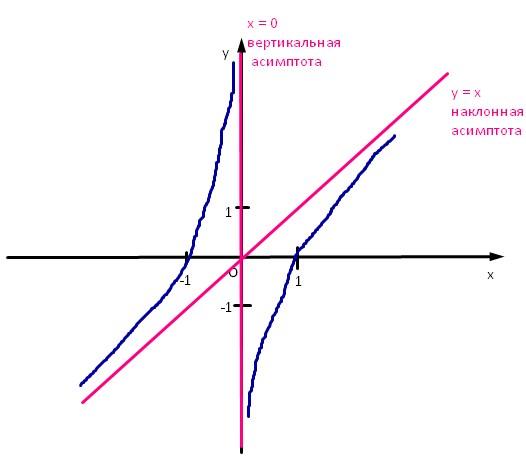
10) Учитывая проведенное исследование строим график функции, т.к. функция нечётная, то левая часть графика симметрична правой относительно начала координат.

у=(х ⁴ -1)/х³

Задание:

Решить №1(а), №2(а), №3(а), №4(а)

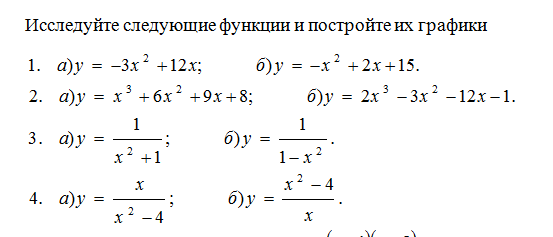
Домашнее задание №№ 1-4 под (б)

Фотоотчёт на ЛС

На следующем уроке каждый из вас будет строить свой график. Поэтому дома разберитесь, ещё раз повторите алгоритмы нахождения монотонности, экстремумов и выпуклости. Если кто-то забыл определение чётной и нечётной функции – смотрите лекции за 1 семестр.

Через занятие будет контрольная работа по производной.