
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Формулировка задачи
2. Формулировка задачи
Введем декартовы 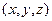 и сферические координаты
и сферические координаты 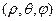 .
.
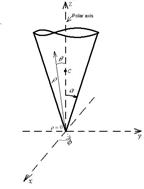
Рис. 1. Декартовы и сферические координаты для нашей задачи
Рассмотрим жидкость, покоющуюся в безграничном конусе (Рис. 1). Добавим стокслет на ось конуса, в точку 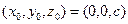 в декартовой системе координат. Стокслет – это точечная сила, приводящая в движение жидкость. Он задается соответствующим тензором Озеена, являющимся функцией Грина, и определяет векторное поле скоростей течения [2]
в декартовой системе координат. Стокслет – это точечная сила, приводящая в движение жидкость. Он задается соответствующим тензором Озеена, являющимся функцией Грина, и определяет векторное поле скоростей течения [2]
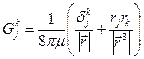 ,
, 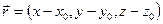 . (1)
. (1)
Компоненты скоростей в направлениях 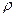 ,
, 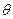 и
и 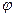 могут быть найдены через преобразования физических координат вектора (Корн, 1968). Ограничимся рассмотрением осесимметричного случая, т.е. компоненты скоростей стокслета зависят лишь от
могут быть найдены через преобразования физических координат вектора (Корн, 1968). Ограничимся рассмотрением осесимметричного случая, т.е. компоненты скоростей стокслета зависят лишь от 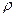 и
и 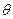 . Среди трех возможных видов стокслеты только один удовлетворяет условию
. Среди трех возможных видов стокслеты только один удовлетворяет условию 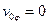 . Это стокслет с компонентами
. Это стокслет с компонентами 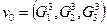 . Тогда компоненты в направлениях
. Тогда компоненты в направлениях 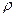 ,
, 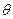 и
и 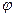 выглядят следующим образом:
выглядят следующим образом:
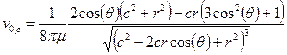 ,
,
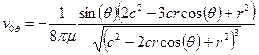 ,
,
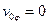 . (2)
. (2)
Поток Стокса в осесимметричном случае характеризуется функцией тока 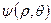 [7]. Компоненты скоростей в этом случае:
[7]. Компоненты скоростей в этом случае:
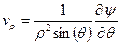 ,
,
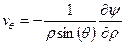 . (3)
. (3)
Интересно найти линии тока жидкости, движимой стокслетом 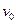 . Поставим задачу. Уравнение Стокса в осесимметричном случае следующее:
. Поставим задачу. Уравнение Стокса в осесимметричном случае следующее:
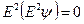 , (4)
, (4)
где оператор 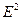 называется оператором Стокса и определен следующим образом:
называется оператором Стокса и определен следующим образом:
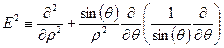 . (5)
. (5)
Предположим, что конус непроницаем, и на его границе выполняются условия прилипания 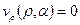 и
и 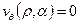 .
.
Обратимся еще раз к стокслету 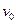 . Используя (3), заметим
. Используя (3), заметим 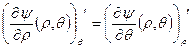 . Таким образом, решив, например, уравнение в полных дифференциалах, можно найти функцию
. Таким образом, решив, например, уравнение в полных дифференциалах, можно найти функцию 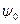 стокслета
стокслета 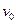 , действующего во всем пространстве:
, действующего во всем пространстве:
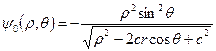 . (6)
. (6)
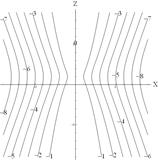
Рис.2. Линии тока стокслета, расположенного в точке 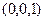 , действующего в неограниченном пространстве
, действующего в неограниченном пространстве
Тогда общая функция тока будет иметь две аддитивные компоненты 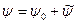 . Оператор
. Оператор 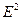 линеен, следовательно
линеен, следовательно 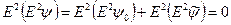 . Граничные условия:
. Граничные условия: 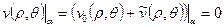 . Можно убедиться, что функция тока
. Можно убедиться, что функция тока 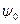 удовлетворяет уравнению Стокса
удовлетворяет уравнению Стокса 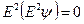 . Зная функцию тока
. Зная функцию тока 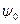 и компоненты скоростей стокслета
и компоненты скоростей стокслета 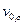 и
и 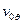 , переформулируем задачу
, переформулируем задачу
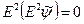
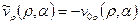 ,
, 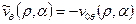 . (7)
. (7)
Общее решение уравнения (7) известно [7]
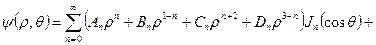
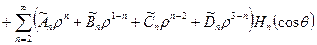 , (8)
, (8)
где 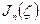 и
и 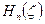 - функции Гегенбауэра первого и второго рода, соответственно. Они линейно связаны с функциями Лежандра
- функции Гегенбауэра первого и второго рода, соответственно. Они линейно связаны с функциями Лежандра 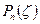 и
и 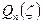 :
:
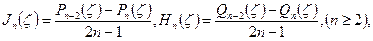
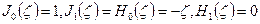 . (9)
. (9)
Поскольку нас интересует гладкое решение (в природе переформулированной задачи нет особенностей), то все коэффициенты с волной должны быть равны нулю [7], тогда компоненты скорости движения жидкости имеют вид:
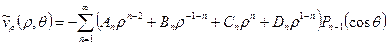 ,
,
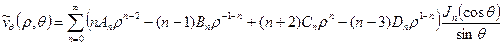 . (10)
. (10)
Оставшиеся коэффициенты определим из двух граничных условий. Предположим, что в нуле, 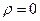 , особенности нет. Тогда
, особенности нет. Тогда 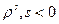 не участвуют в искомом решении и в компонентах скоростей, и функция тока
не участвуют в искомом решении и в компонентах скоростей, и функция тока 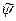 выглядит следующим образом
выглядит следующим образом
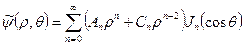 ,
,
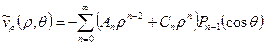 ,
,
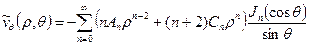 . (11)
. (11)
Разложим компоненты скоростей на границе по ортогональным полиномам Лагерра. Поскольку система полиномов Лагерра с весовой функцией 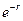 полна в пространстве
полна в пространстве 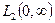 , то произвольная функция
, то произвольная функция 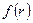 , определённая на промежутке
, определённая на промежутке 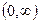 и удовлетворяющая некоторым условиям, которые будут описаны ниже, может быть представлена в виде бесконечного ряда по полиномам Лагерра [13]
и удовлетворяющая некоторым условиям, которые будут описаны ниже, может быть представлена в виде бесконечного ряда по полиномам Лагерра [13]
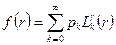 ,
, 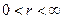 , (12)
, (12)
где коэффициенты 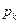 определяются следующим образом:
определяются следующим образом:
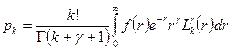 . (13)
. (13)
Существует теорема, утверждающая, что если функция 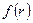 кусочно-гладкая на всяком открытом интервале
кусочно-гладкая на всяком открытом интервале 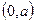 и, кроме того, интеграл
и, кроме того, интеграл 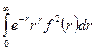 имеет конечное значение, то ряд (12) с коэффициентами (13) сходится, и его сумма равна
имеет конечное значение, то ряд (12) с коэффициентами (13) сходится, и его сумма равна 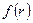 в каждой точке
в каждой точке 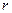 , где эта функция непрерывна. Для конкретных значений параметров угла раствора конуса
, где эта функция непрерывна. Для конкретных значений параметров угла раствора конуса 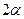 и расположения стокслета, точки
и расположения стокслета, точки 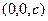 , можно убедиться в том, что функции скоростей стокслета на границе конуса
, можно убедиться в том, что функции скоростей стокслета на границе конуса 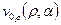 и
и 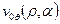 непрерывны и удовлетворяют условиям теоремы, следовательно, разложение по полиномам Лагерра имеет место и выглядит следующим образом:
непрерывны и удовлетворяют условиям теоремы, следовательно, разложение по полиномам Лагерра имеет место и выглядит следующим образом:
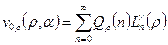 ,
,
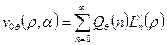 .
.
Попробуем также разложить по полиномам Лагерра компоненты составляющей скорости жидкости 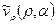 и
и 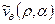 на границе:
на границе:
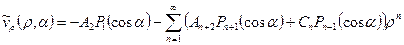 ,
,
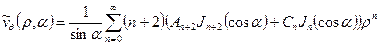 . (15)
. (15)
Для этого воспользуемся известным разложением степенной функции по полиномам Лагерра. В частности, если показатель степени – целое положительное число, то ряд содержит конечное число членов
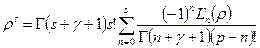 ,
,
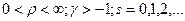 (16)
(16)
Проведем разложение по простейшим полиномам Лагерра, то есть по таким полиномам 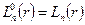 , для которых
, для которых 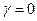 . Тогда выражение для степенной функции упрощается:
. Тогда выражение для степенной функции упрощается:
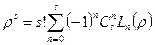 . (17)
. (17)
Теперь будем рассматривать конечные суммы из 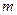 слагаемых ряда вместо бесконечных сумм, и после некоторых преобразований получаем следующие выражения для скоростей на границе: разложение скоростей стокслета
слагаемых ряда вместо бесконечных сумм, и после некоторых преобразований получаем следующие выражения для скоростей на границе: разложение скоростей стокслета 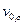 и
и 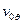 :
:
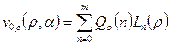 ,
,
 ,
,
разложение дополнительных компонент скорости 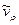 и
и 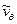 :
:
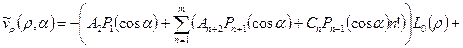
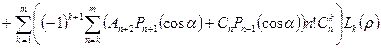 ,
,
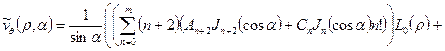
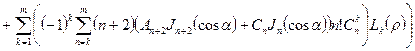 , (19)
, (19)
и после некоторых преобразований получим системы линейных алгебраических уравнений для отыскания соответствующих констант.
Далее аргумент 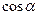 функций Лежандра и функций Гегенбауэра опустим для краткости.
функций Лежандра и функций Гегенбауэра опустим для краткости.
Система для определения коэффициентов 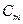 и
и 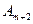 :
:
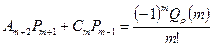 ,
,
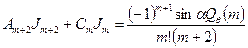 .
.
Последующие коэффициенты можно последовательно найти, используя уже вычисленные, то есть, для любого 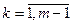 :
:
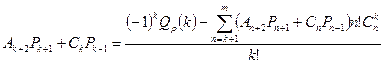 ,
,
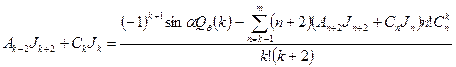 . (21)
. (21)
Последние несколько коэффициентов находятся однозначно через все предыдущие
 ,
,
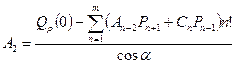 ,
,
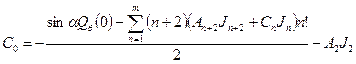 . (22)
. (22)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|