
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лекция. Формула полной вероятности. Формула Байеса.
Лекция. Формула полной вероятности. Формула Байеса.
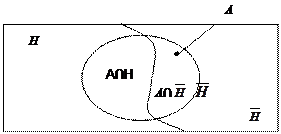 |
Рассмотрим два события А и Н. Каковы бы ни были взаимоотношения между событиями А и Н, всегда можно сказать, что вероятность события А равна вероятности пересечения событий А и Н плюс вероятность пересечения А и дополнения Н (событие
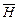 ). Поясним сказанное на диаграмме Венна (рис.1). Разложение А на части зависит от
). Поясним сказанное на диаграмме Венна (рис.1). Разложение А на части зависит от 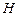 и
и 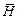 . Р(А) = Р(А
. Р(А) = Р(А 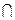 Н) + Р(А∩
Н) + Р(А∩ 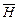 ).
).
Рис. 1. Диаграмма Венна к формуле (1)
Наборы 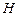 и
и 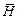 – форма расчленения набора A на два подмножества взаимно несовместных событий. События Н и
– форма расчленения набора A на два подмножества взаимно несовместных событий. События Н и 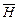 взаимно противоположны. Событие А может произойти либо с Н, либо с
взаимно противоположны. Событие А может произойти либо с Н, либо с 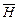 , но не с двумя вместе (см. рис. 1).
, но не с двумя вместе (см. рис. 1).
Рассмотрим более сложный случай. Пусть событие А может осуществляться лишь вместе с одним из событий Н1, H2, H3,..., Hn, образующих полную группу, т. е. эти события являются единственно возможными и несовместными (рис. 2). Так как заранее неизвестно, какое из событий Н1, H2, H3,..., Hn наступит, то их называют гипотезами. Пусть также известны вероятности гипотез Р(Н1), Р(Н2),…, Р(Hn) и условные вероятности события А, а именно: Р(А/Н1), Р(А/Н2),…, Р(А/Нn).
Так как гипотезы образуют полную группу, то 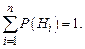
Рассмотрим событие А – это или Н1·А, или … Нn·А. События Н1·А, Н2·А, …, Нn·А – несовместные попарно, так как события Н1, H2, H3,..., Hn попарно несовместны. К этим событиям применяем теорему сложения вероятностей для несовместных событий:
Р(А)=Р(Н1·А)+Р(Н2·А) +…+ Р(Нn ·А) = 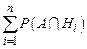 .
.
События Н1 и А, Н2 и А,..., Нn и А – зависимые. Применив теорему умножения вероятностей для зависимых событий, получим (рис. 2):
Р(А) = Р(Н1)∙Р(А/Н1)+ Р(Н2)∙Р(А/Н2) +...+Р(Нn)∙Р(А/Нn) = 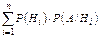 .
.
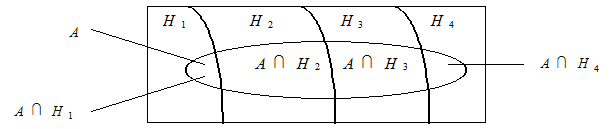
Рис. 2. Событие А может осуществляться лишь с одним
из событий Н1, Н2, ..., Нn, образующих полную группу событий
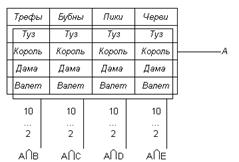 Проиллюстрируем сказанное на примере с колодой карт. Определим А как событие, состоящее в извлечении карты с картинкой (т. е. карты с изображением или туза, или короля, или дамы, или валета). Пусть события В, С, D, Е означают извлечение карт различной масти («трефы», «бубны», «черви», «пики»). Мы можем сказать, что вероятность извлечь из колоды карту с изображением туза, короля, дамы или валета есть Р(А) = Р(А∩В) + Р(А∩С) + Р(А∩D) + Р(А∩Е) = 4/52 + 4/52 + 4/52+4/52 = 16/52. Это означает, как мы уже знаем, вероятность извлечения карты с картинкой из колоды в 52 карты. Событие А представляет собой набор, составленный из пересечений А с наборами В, С, D, Е (рис. 3). Рис. 3. Пример с колодой карт
Проиллюстрируем сказанное на примере с колодой карт. Определим А как событие, состоящее в извлечении карты с картинкой (т. е. карты с изображением или туза, или короля, или дамы, или валета). Пусть события В, С, D, Е означают извлечение карт различной масти («трефы», «бубны», «черви», «пики»). Мы можем сказать, что вероятность извлечь из колоды карту с изображением туза, короля, дамы или валета есть Р(А) = Р(А∩В) + Р(А∩С) + Р(А∩D) + Р(А∩Е) = 4/52 + 4/52 + 4/52+4/52 = 16/52. Это означает, как мы уже знаем, вероятность извлечения карты с картинкой из колоды в 52 карты. Событие А представляет собой набор, составленный из пересечений А с наборами В, С, D, Е (рис. 3). Рис. 3. Пример с колодой карт
Вывод.Если событие А может наступить только вместе с одним из событий Н1, Н2, Н3, ..., Нn, образующих полную группу несовместных событий и называемых гипотезами, то вероятность события А равна сумме произведений вероятностей каждого из событий Н1, Н2, Н3, ..., Нn на соответствующую условную вероятность события А.
Случай двух событий: 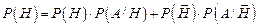 .
.
Случай более чем двух событий: 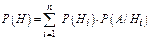 , где i = 1, 2, ..., п.
, где i = 1, 2, ..., п.
Пример. Экономист полагает, что вероятность роста стоимости акций некоторой компании в следующем году будет равна 0,75, в случае успешного развития экономики страны, и эта же вероятность составит 0,30, если произойдет спад экономики. По его мнению, вероятность экономического подъема в будущем году равна 0,80. Используя предположения экономиста, оцените вероятность того, что акции компании поднимутся в цене в следующем году.
Решение:Событие А – «акции компании поднимутся в цене в будущем году». Составим рабочую таблицу:
| Hi | Гипотезы Hi | Р(Hi) | P(А/Hi) | Р(Hi)P(А/Hi) |
| H1 – «подъем экономики» | 0,80 | 0,75 | 0,60 | |
| H2 – «спад экономики» | 0,20 | 0,30 | 0,06 | |
| ∑ | 1,00 | – | P(А) = 0,66 | |
Пример.В каждой из двух урн содержится 6 черных и 4 белых шара. Из урны 1 в урну 2 наудачу переложен один шар. Найти вероятность того, что шар, извлеченный из урны 2 после перекладывания, окажется черным.
Решение:Событие А – «шар, извлеченный из урны 2, – черный». Составим рабочую таблицу:
| Hi | Гипотезы Hi | Р(Hi) | P(А/Hi) | Р(Hi)P(А/Hi) |
| H1 – «из урны 1 в урну 2 переложили черный шар» | 6/10 | 7/11 | 42/110 | |
| H2 – «из урны 1 в урну 2 переложили белый шар» | 4/10 | 6/11 | 24/110 | |
| ∑ | 1,00 | – | Р(А) = 0,60 | |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|