
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задачи с практическим содержанием
Задачи с практическим содержанием
Решение многих практических задач часто сводится к определению наибольшего и наименьшего значения функции на отрезке. Ведь и возникновение математического анализа явилось следствием из необходимости решать практические задачи на нахождение оптимальных значений величин, например:
- увеличение урожайности с гектара пашни;
- получение балки с наибольшим прямоугольным сечением из круглого бревна;
- ограждение земельного участка наибольшей площади изгородью заданной длины и т. д.
Поэтому целью нашего урока является систематизация навыков и умений учащихся по применению знаний, полученных в ходе изучения темы «Производная и ее применение» к решению задач этого типа, а так же для решения различных физических задач.
ЗАДАЧА 1: Заготовлена изгородь длиной 480м. Этой изгородью надо огородить с трех сторон, примыкающий к реке, участок. Какова должна быть ширина и длина участка, чтобы его площадь была наибольшей при заданной длине изгороди?
РЕШЕНИЕ:
 S=AB·BC
S=AB·BC
Пусть АВ=х, тогда ВС= 480-2х
S(х) = х · (480 - 2х) = 480х - 2х2
D(х) = (0;240), т. к. S(х) > 0
480х – 2х2 > 0
2х · (240 – х) > 0
х1 = 0, х2 = 240
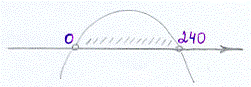
0 < х < 240
S¢ (x) = 480 - 4x
S ¢(x) = 0, 480 - 4x =0
x = 120

Т. о. Smax = S (120) = 28800м2 при АВ = 120м и ВС = 240м
Ответ: при ширине 120м и длине 240м площадь участка будет наибольшей.
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ :
- определить исследуемую функцию;
- ввести переменную;
- установить область определения функции;
- вычислить max/min функции на заданном интервале.
ЗАДАЧА 2: Дан прямоугольный лист жести (АВ = 80см, ВС = 50см). Надо вырезать около всех углов одинаковые квадраты так, чтобы после загибания оставшихся кромок получилась открытая сверху коробка максимальной вместимости.
РЕШЕНИЕ:
 V(x) = ( 80-2x)( 50-2x)x = 4x3 – 260x2 – 4000x
V(x) = ( 80-2x)( 50-2x)x = 4x3 – 260x2 – 4000x
D(V) = (0;25), т. к. V(x) > 0
( 80-2x)( 50-2x)x > 0
x1 = 40, x2 = 25, x3 = 0

0 < x < 25
V′ (x) = 12x2 – 520x + 4000
V′ (x) = 0, 12x2 – 520x + 4000 = 0
3x2 – 130x + 1000 = 0
D = 4900
x1 = 10, x2 = 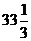
x1 Є (0;25)
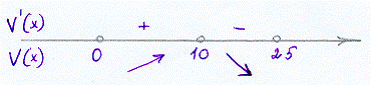
Vmax (x) = V(10) = 1800см3
Ответ: Объем коробки будет максимальным, если сторона вырезаемого квадрата равна 10см.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|