Практическая работа №8.. Тема: «Приближенное вычисление по формулам прямоугольников, трапеции, Симпсона». Теоретическая часть. Метод прямоугольников

Практическая работа №8.

Тема: «Приближенное вычисление по формулам прямоугольников, трапеции, Симпсона»

Цель работы:

выработать навыки применения формул прямоугольников, трапеций и Симпсона для вычисления определенных интегралов.

Теоретическая часть

Метод прямоугольников

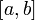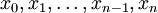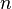Пусть требуется определить значение интеграла функции на отрезке . Этот отрезок делится точками на равных отрезков длиной 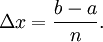Обозначим через 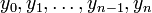значение функции 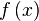в точках 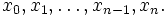Далее составляем суммы 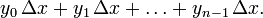Каждая из сумм — интегральная сумма для 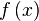на 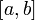и поэтому приближённо выражает интеграл

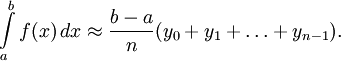
Если заданная функция — положительная и возрастающая, то эта формула выражает площадь ступенчатой фигуры, составленной из «входящих» прямоугольников, также называемая формулой левых прямоугольников, а формула

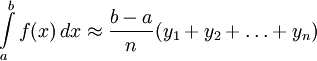
выражает площадь ступенчатой фигуры, состоящей из «выходящих» прямоугольников, также называемая формулой правых прямоугольников. Чем меньше длина отрезков, на которые делится отрезок 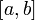, тем точнее значение, вычисляемое по этой формуле, искомого интеграла.

Очевидно, стоит рассчитывать на бо́льшую точность если брать в качестве опорной точки для нахождения высоты точку посередине промежутка. В результате получаем формулу средних прямоугольников:

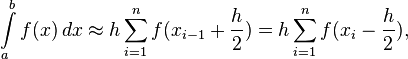
где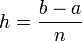

Вычислить определенный интеграл

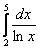
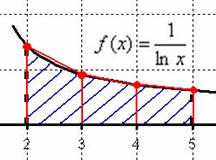
в данном примере интеграл не берётся – перед нами неберущийся, так называемый интегральный логарифм. А существует ли вообще этот интеграл? Изобразим на чертеже график подынтегральной функции :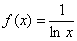

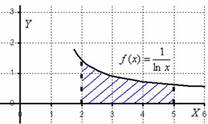
Всё нормально. Подынтегральная функция непрерывна на отрезке 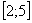и определенный интеграл 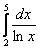численно равен заштрихованной площади. Да вот только интеграл не берётся. И в подобных случаях на помощь как раз приходят численные методы.

Существуют несколько основных методов приближенного вычисления определенного интеграла, который встречается в задачах:

Метод прямоугольников.

Отрезок интегрирования разбивается на несколько частей и строится ступенчатая фигура, которая по площади близка к искомой площади:

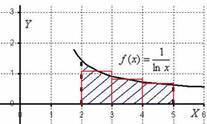
В данном примере проведено разбиение отрезка интегрирования 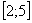на три отрезка:
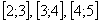. Очевидно, что чем чаще разбиение (больше более мелких промежуточных отрезков), тем выше точность. «Ступенчатое» приближение является самым простым, и, видимо, поэтому довольно редко встречается в практических задачах.

Метод трапеций.

Идея аналогична. Отрезок интегрирования разбивается на несколько промежуточных отрезков, и график подынтегральной функции приближается ломаной линией:

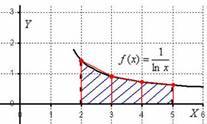
Таким образом, наша площадь (синяя штриховка) приближается суммой площадей трапеций (красный цвет). Отсюда и название метода.

Метод Симпсона (метод парабол).

Это более совершенный способ – график подынтегральной функции приближается не ломаной линией, а маленькими параболками. Сколько промежуточных отрезков – столько и маленьких парабол. Если взять те же три отрезка, то метод Симпсона даст ещё более точное приближение, чем метод прямоугольников или метод трапеций.

Визуально приближение будет накладываться на график функции 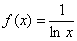(ломаная линия предыдущего пункта – и то практически совпала).

Как вычислить определенный интеграл методом трапеций?

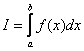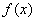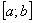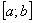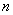Рассмотрим определенный интеграл , где – функция, непрерывная на отрезке . Проведём разбиение отрезка на равных отрезков:
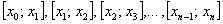. При этом, очевидно: 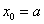(нижний предел интегрирования) и 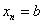(верхний предел интегрирования). Точки 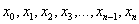также называют узлами.

Тогда определенный интеграл можно вычислить приближенно по формуле трапеций:
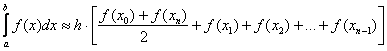, где:
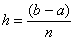– длина каждого из маленьких отрезков или шаг;
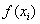– значения подынтегральной функции в точках .

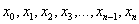Пример 1

Вычислить приближенно определенный интеграл по формуле трапеций. Результаты округлить до трёх знаков после запятой.
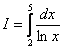,разбив отрезок интегрирования на 3 части.

Решение:

По условию отрезок интегрирования нужно разделить на 3 части, то есть .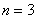
Вычислим длину каждого отрезка разбиения: 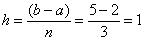. Параметр 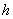, напоминаю, также называют шагом.

Сколько будет точек 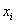(узлов разбиения)? Их будет на одну больше, чем количество отрезков:

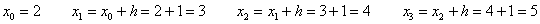
Ну а общая формула трапеций:

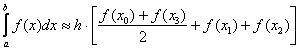
Для расчетов можно использовать обычный микрокалькулятор:

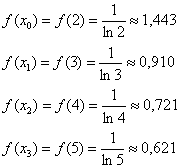
Обратите внимание, что, в соответствии с условием задачи, все вычисления следует округлять до 3-го знака после запятой.

Окончательно:

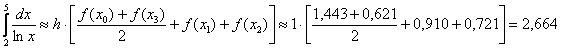
С геометрической точки зрения мы вычислили сумму площадей трёх трапеций (см. рис. выше).

Формула Симпсона для приближенного вычисления определенного интеграла имеет следующий вид:
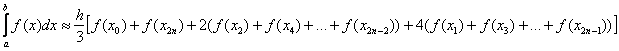, где:
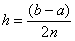– длина каждого из маленьких отрезков или шаг;
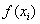– значения подынтегральной функции в точках .

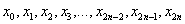Детализируя это нагромождение, разберу формулу подробнее:
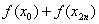– сумма первого и последнего значения подынтегральной функции;
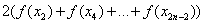– сумма членов с чётными индексами умножается на 2;
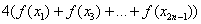– сумма членов с нечётными индексами умножается на 4.

Пример2 : Вычислить приближенно определенный интеграл по формуле Симпсона с точностью до 0,0001. Разбиение начать с двух отрезков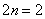

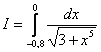
Решение:1) Рассмотрим два отрезка разбиения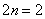
Вычислим шаг: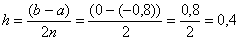
Заполним расчетную таблицу:

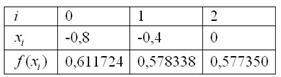
Таким образом:

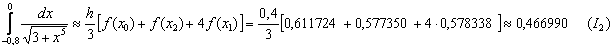
2) Рассмотрим четыре отрезка разбиения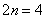
Вычислим шаг: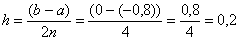
Заполним расчетную таблицу:

Таким образом:

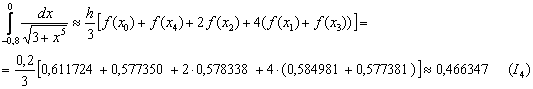
Оценим погрешность:

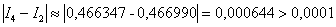
Примечание: если оценку проводить по правилу Рунге, то: 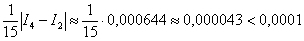, то есть вычисления закончены и дополнительного шага не требуется.

ХОД РАБОТЫ Внимательно изучите теоретическую часть практической работы, основные и дополнительные источники и дайте развёрнутые ответы на контрольные вопросы: 1. В чём суть метода прямоугольников. 2. В чём суть метода трапеций, приведите примеры. 3. В суть метода Симпсона, приведите примеры.

Основные источники:

1. Григорьев С.Г., Иволгина С.В. «Математика»: учебник для студ. образоват. учреждений сред.проф. образования под редакцией В.А. Гусева. – 10-е изд., стер. – М.: Издательский центр «Академия», 2018.

Дополнительные источники:

2. Богомолов Н.В., Самойленко П.И. «Математика» учебник для средних спец. учебных заведений -5 изд., переработанное и доп. – М.: издательство Юрайт, 2015.

3. Богомолов Н.В. практические занятия по математике: учебное пособие для СПО / Н.В. Богомолов. – 11-е изд., перераб. И доп. –М.: издательство Юрайт, 2015.

4. Федеральное хранилище Единой коллекции цифровых образовательных ресурсов [Электронный ресурс] / Национальный фонд подготовки кадров – Электрон.дан. – Режим доступа: http://school-collection.edu.ru/catalog/– Загл. с экрана;

5. Единое окно доступа к образовательным ресурсам [Электронный ресурс]: каталог образовательных Интернет - ресурсов/ ФГУ ГНИИ ИТТ «Информика». – Электрон.дан. – Режим доступа: http://window.edu.ru/– Загл. с экрана