Пример № 1. Пример № 2. Пример № 3

ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ 2 ДМС 2021

МЕТОД ОСРЕДНЕНИЯ

Пример № 1

Найти методом осреднения приближённое решение в первом по малому параметру приближении уравнений свободных колебаний груза на горизонтальной плоскости рис. 1 под действием упругой силы пружины и кулоновой силы трения

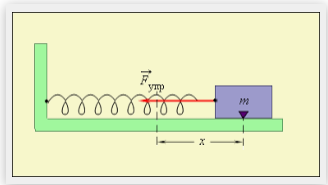
Рис. 1 Груз на шероховатой плоскости

Ось x направлена по горизонтали, начало отсчёта находится в положении равновесия груза.

Масса груза M=10^-²кг, коэффициент жёсткости пружины K=20 кг с^-2, коэффициент трения груза о плоскость f=0,02, x(0)=3,5 10^-2 м, 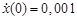м с^-1

|Fтр|=f M 9,8= 0,00196 Н

ε= f M 9,8/(K x(0)|=0,0028

Пример № 2

Найти методом осреднения приближённое решение в первом по малому параметру приближении уравнений свободных колебаний груза рис. 2 под действием упругой силы пружины и силы вязкого сопротивления, пропорциональной первой степени скорости груза.

Ось x направлена по вертикали, начало отсчёта находится в положении равновесия груза.

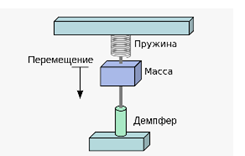
Рис. 2 Груз, подвешенный с помощью упруго-демпфирующего элемента

Масса груза M=10^-2кг, коэффициент жёсткости пружины K=20 кг с^-2, коэффициент демпфирования R= 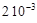кг с^-1, x(0)=3,5 10^-3 м, 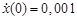м с^-1 .

Fсопр=R 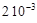v= v;

ε=R /K / 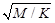=0,0045

Пример № 3

Найти методом осреднения приближённое решение в первом по малому параметру приближении уравнения движения тела под действием линейной упругой силы и силы аэродинамического сопротивления, пропорциональной второй степени скорости тела.

Масса тела M=10³кг, коэффициент упругости K=3 10² кг с^-2, коэффициент пропорциональности силы сопротивления квадрату скорости 𝜇 = 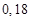кг/ м, x(0)=2,5 10^-3 м, 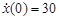м с^-1

Fсопр= 𝜇 v²=0,18 v²;

ε= 𝜇 / x(0)/M=4.5 10^-6

ЛИТЕРАТУРА

Новожилов И.В. Фракционный анализ. М: Изд-во механико-математического факультета МГУ, 1995.