Дополнение к Заданию. на выполнение курсовой работы. по дисциплине «Дифференциальные уравнения»

Дополнение к Заданию

на выполнение курсовой работы

по дисциплине «Дифференциальные уравнения»

1. Значения 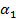и 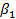заданы в таблице вариантов:

\

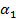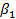
(указанный в таблице вариант соответствуют номеру студента в группе по журналу).

2. Таблица (примерная) значений :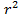

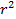
0,01

0,1

0,5

предложена лишь в качестве ориентира при выборе значений параметра 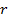, при назначении которых следует добиваться максимальной изобразительной ясности в отношении характера эволюции собственной функции.

В задаче (–) следует найти значение параметра 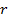, соответствующее нулевому собственному значению и соответствующую собственную функцию и определить характер изменения первой собственной функции, соотвтствующей отрицательному первому собственному значению.

Обратить внимание на местоположение нулей собственных функций (в том числе взаимное расположение нулей собственных функций, соответствующих различным собственным значениям).

3. При оформлении Курсовой работы графики собственных функций, соответствующие собственным значениям 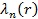, , 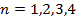при фиксированном 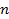и различных 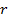(см. п.2), следует изобразить на одном рисунке. При изменении параметра 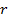, применить, по возможности, компьютерную анимацию.

4. Для изображения собственных функций следует применить два способа нормировки, так чтобы:

1) были выполнены условия , ;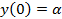

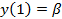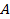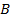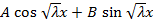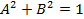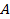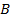2) коэффициенты и собственной функция вида , удовлетворяли условию (выбор возможных знаков и определяется требованием наглядности).

5. Литература: Покровский И.Л., О задаче на собственные значения для оператора Лапласа с нелокальными граничными условиями, Дифференциальные уравнения, т.54, 2018, №10, с.1391-1398 (текст статьи передан в группы по электронной почте).