
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Домашнее задание по алгебре на 17.05.2021
Домашнее задание по алгебре на 17.05.2021
1. Задание 1
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответе запишите полученную последовательность четырёх цифр.
| Населённые пункты | Кулаки | Илькино | Осинки | Кудрино |
| Цифры |
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
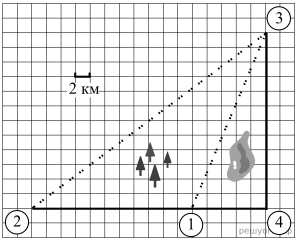
Решение.
Пользуясь описанием и рисунком можно заметить, что деревня Кулаки соответствует цифре 4, деревня Илькино — цифре 1, деревня Осинки — цифре 2 и деревня Кудрино —цифре 3.
Ответ: 4123.
Ответ: 4123
2. Задание 2
Найдите расстояние от деревни Осинки до села Кудрино по прямой. Ответ выразите в километрах.
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.

Решение.
Расстояние от деревни Осинки до села Кудрино соответствует длине гипотенузы прямоугольного треугольника с катетами 32 и 24. По теореме Пифагора имеем:

Ответ: 40.
Ответ: 40
3. Задание 3
Сколько километров проедут Гена с дедушкой, если они поедут по шоссе через деревню Кулаки?
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.

Решение.
Расстояние, которое проедут Гена с дедушкой, проезжая через Кулаки, равно сумме длин катетов прямоугольного треугольника с катетами 32 и 24. Таким образом, имеем, что искомое расстояние равно 32 + 24 = 56.
Ответ: 56.
Ответ: 56
4. Задание 4
Сколько времени затратят на дорогу Гена с дедушкой, если они поедут сначала до Илькино, а затем свернут на грунтовую дорогу, идущую мимо озера? Ответ выразите в минутах.
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.

Решение.
По шоссе Гена с дедушкой проедут 22 километра со скоростью 60 км/ч. Следовательно, они затратят 22 : 60 = 0,37 часа или 22 минуты. Дальше по условию задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы прямоугольного треугольника с катетами 24 и 10. Таким образом, по теореме Пифагора длина составит:

По грунтовой дороге Гена с дедушкой едут со скоростью 40 км/ч, следовательно они затратят 26 : 40 = 0,65 часа или 39 минут.
Таким образом, Гена с дедушкой на весь путь затратят 22 + 39 = 61 минута.
Ответ: 61.
Ответ: 61
5. Задание 5
Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Гена с дедушкой, если поедут этим маршрутом.
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.

Решение.
Гена с дедушкой могут поехать тремя разными маршрутами. Рассмотрим каждый из них.
1) По грунтовой дороге напрямую. Длина такого пути соответствует длине гипотенузы прямоугольного треугольника с катетами 32 и 24. По теореме Пифагора имеем:

Двигаясь по грунтовой дороге со скоростью 40 км/ч дедушка с Геной потратят 40 : 40 = 1 час или 60 минут.
2) Сначала по шоссе, а затем по грунтовой дороге вдоль озера. По шоссе Гена с дедушкой проедут 22 километра со скоростью 60 км/ч. Следовательно, они затратят 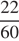 часа или 22 минуты. Дальше по условию задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы прямоугольного треугольника с катетами 24 и 10. Таким образом, по теореме Пифагора длина составит:
часа или 22 минуты. Дальше по условию задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы прямоугольного треугольника с катетами 24 и 10. Таким образом, по теореме Пифагора длина составит:

По грунтовой дороге Гена с дедушкой едут со скоростью 40 км/ч, следовательно они затратят 26 : 40 = 0,65 часа или 39 минут.
Таким образом, Гена с дедушкой на весь путь затратят 22 + 39 = 61 минута.
3) По шоссе через Кулаки. Расстояние, которое проедут Гена с дедушкой, проезжая через Кулаки, равно сумме длин катетов прямоугольного треугольника с катетами 32 и 24. Таким образом, имеем, что искомое расстояние равно 32 + 24 = 56.
Двигаясь по шоссе со скоростью 60 км/ч, Гена с дедушкой потратят 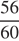 часа или 56 минут.
часа или 56 минут.
Таким образом, самый быстрый путь составит 56 минут.
Ответ: 56.
Ответ: 56
6. Задание 6
Найдите значение выражения 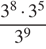 .
.
Решение.
Найдем значение выражения:
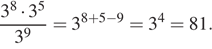
Ответ: 81.
Ответ: 81
7. Задание 7
На координатной прямой отмечены числа x и y.

Какое из приведённых утверждений неверно?
В ответе укажите номер правильного варианта.
1) 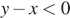
2) 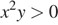
3) 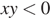
4) 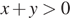
Решение.
Заметим, что 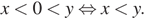 Число
Число 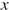 располагается ближе к нулю, чем число
располагается ближе к нулю, чем число 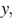 следовательно,
следовательно, 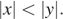 Рассмотрим каждое утверждение:
Рассмотрим каждое утверждение:
1) 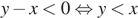 — неверно.
— неверно.
2) 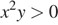 — верно.
— верно.
3) 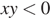 — верно.
— верно.
4) 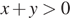 — верно.
— верно.
Ответ указан под номером: 1.
Ответ: 1
8. Задание 8
Упростите выражение 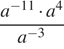 и найдите его значение при
и найдите его значение при  . В ответе запишите полученное число.
. В ответе запишите полученное число.
Решение.
Упростим выражение:

При  , значение полученного выражения равно 16.
, значение полученного выражения равно 16.
Ответ: 16.
Ответ: 16
9. Задание 9
Решите уравнение 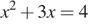 .
.
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение.
Запишем уравнение в виде 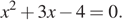 По теореме, обратной теореме Виета, сумма корней равна −3, а их произведение −4.
По теореме, обратной теореме Виета, сумма корней равна −3, а их произведение −4.
Тем самым это числа −4 и 1.
Ответ: −41.
Ответ: -41
-41
10. Задание 10
Родительский комитет закупил 20 пазлов для подарков детям в связи с окончанием учебного года, из них 11 с машинами и 9 с видами городов. Подарки распределяются случайным образом между 20 детьми, среди которых есть Илюша. Найдите вероятность того, что Илюше достанется пазл с машиной.
Решение.
Вероятность того, что Коле достанется пазл с машиной равна 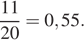
Ответ: 0,55.
Ответ: 0,55
0,55
11. Задание 11

На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция возрастает на промежутке [2; +∞)
2) f( −1 ) < f( 5 )
3) Наименьшее значение функции равно −9
Решение.
Проверим каждое утверждение.
1) На луче [2; +∞) большему значению аргумента сответствует большее значение функции. Следовательно, функция возрастает на этом луче; первое утверждение верно.
2) Значения фунцкии в точках −1 и 5 равны нулю, поэтому f(−1) = f(5). Второе утверждение неверно.
3) Наименьшее значение функции равно −9. Третье утверждение верно.
Ответ: 2.
Ответ: 2
12. Задание 12
Полную механическую энергию тела (в джоулях) можно вычислить по формуле 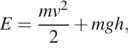 где
где 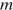 — масса тела (в килограммах),
— масса тела (в килограммах), 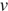 — его скорость (в м/с),
— его скорость (в м/с), 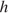 — высота положения центра масс тела над произвольно выбранным нулевым уровнем (в метрах), а
— высота положения центра масс тела над произвольно выбранным нулевым уровнем (в метрах), а 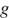 — ускорение свободного падения (в м/с2). Пользуясь этой формулой, найдите
— ускорение свободного падения (в м/с2). Пользуясь этой формулой, найдите 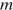 (в килограммах), если
(в килограммах), если 
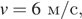
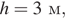 а
а 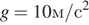
Решение.
Выразим массу: 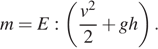 Подставим значения переменных:
Подставим значения переменных:
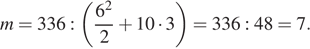
Ответ: 7.
Ответ: 7
13. Задание 13
На каком рисунке изображено множество решений неравенства  ?
?
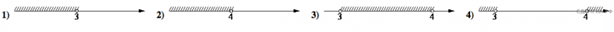
Решение.
Решим неравенство:
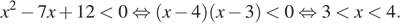
Ответ: 3.
Ответ: 3
14. Задание 14
Грузовик перевозит партию щебня массой 90 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 2 тонны щебня. Определите, сколько тонн щебня было перевезено за десятый день, если вся работа была выполнена за 12 дней.
Решение.
Пусть в первый день грузовик перевез  тонны щебня, во второй —
тонны щебня, во второй — 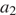 , …, в последний —
, …, в последний — 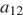 тонн; всего было перевезено
тонн; всего было перевезено  тонны; норма перевозки увеличивалась ежедневно на
тонны; норма перевозки увеличивалась ежедневно на 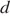 тонн. Таким образом,
тонн. Таким образом,
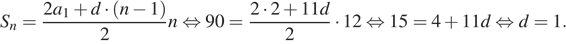
Имеем:

Следовательно, за десятый день было перевезено 11 тонн щебня.
Ответ: 11.
Ответ: 11
15. Задание 15
Сумма двух углов равнобедренной трапеции равна 220°. Найдите меньший угол трапеции. Ответ дайте в градусах.
Решение.
Так как сумма односторонних углов трапеции равна 180°, в условии говорится о сумме углов при основании. Поскольку трапеция является равнобедренной, углы при основании равны. Значит, каждый из них равен 110°. Сумма односторонних углов трапеции равна 180°, поэтому меньший угол равен 180° − 110° = 70°.
Ответ: 70.
Ответ: 70
16. Задание 16
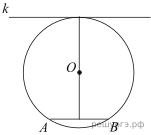
Радиус окружности с центром в точке O равен 65, длина хорды AB равна 66 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
Решение.
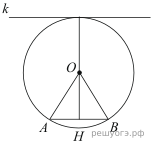
Проведём построение и введём обозначения, как показано на рисунке. Рассмотрим треугольники 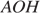 и
и 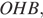 они прямоугольные,
они прямоугольные, 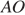 и
и 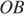 равны как радиусы окружности,
равны как радиусы окружности, 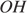 — общая, следовательно, эти треугольники равны. Откуда
— общая, следовательно, эти треугольники равны. Откуда  Из прямоугольного треугольника
Из прямоугольного треугольника 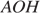 по теореме Пифагора найдём
по теореме Пифагора найдём 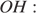

Следовательно, расстояние от хорды до параллельной ей касательной равно 56 + 65 = 121.
Ответ: 121.
Ответ: 121
17. Задание 17
В ромбе сторона равна 10, одна из диагоналей — 10, а угол, лежащий напротив этой диагонали, равен 60°. Найдите площадь ромба, деленную на 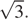
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:

Ответ: 50.
Ответ: 50
18. Задание 18
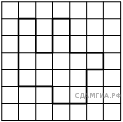
На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.
Решение.
Площадь данной фигуры равна выделенным клеткам. Посчитаем клетки — их 15. Таким образом, площадь равна 15.
Ответ: 15.
Ответ: 15
19. Задание 19
Укажите номера верных утверждений.
1) Если угол острый, то смежный с ним угол также является острым.
2) Диагонали квадрата взаимно перпендикулярны.
3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Если угол острый, то смежный с ним угол также является острым» — неверно, т. к. смежные углы в сумме составляют 180°.
2) «Диагонали квадрата взаимно перпендикулярны» — верно, т. к. квадрат — частный случай ромба.
3) «В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности» — верно, т. к. окружность — это множество точек, находящихся на заданном расстоянии от данной точки.
Ответ: 23.
Ответ: 23
20. Задание 20
Решите систему уравнений
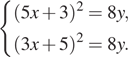
Решение.
Правые части уравнений системы равны, значит,

откуда 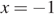 или
или 
При 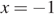 получаем
получаем 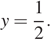 При
При  получаем
получаем 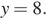
Решения системы уравнений: 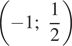 и
и 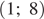
Ответ: 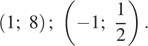
Критерии проверки:
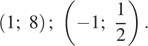
21. Задание 21
Расстояние между городами А и В равно 490 км. Из города А в город В со скоростью 55 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города В выехал со скоростью 90 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?
Решение.
Пусть 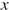 км — искомое расстояние,
км — искомое расстояние,  .
.
Составим таблицу по данным задачи:
Так как второй автомобиль вышел на 1 ч. позже первого, составим уравнение:
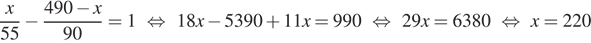
Ответ: 220 км.
Другое решение:
За первый час пути автомобиль, выехавший из города А, проехал 55 километров и расстояние от него до города В стало равным 435 км. Далее, скорость сближения двух автомобилей равна 145 км/ч, значит, они встретятся через 3 часа после выезда второго автомобиля. Таким образом, первый автомобиль до встречи находился в пути 4 часа, и проехал за это время 220 километров.
Ответ: 220 км.
Критерии проверки:
220 км.
22. Задание 22
Постройте график функции 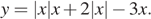 Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Решение.
Раскрывая модуль, получим, что функцию можно представить следующим образом:
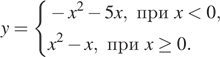
Этот график изображён на рисунке:

Из графика видно, что прямая 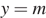 имеет с графиком функции ровно две общие точки при
имеет с графиком функции ровно две общие точки при 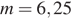 и
и 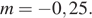
Ответ: −0,25; 6,25.
Критерии проверки:
−0,25; 6,25.
23. Задание 23
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
Решение.
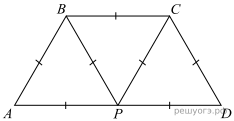 Пусть точка
Пусть точка 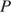 — середина стороны
— середина стороны 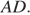 Поскольку
Поскольку 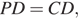 то треугольник
то треугольник 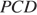 — равнобедренный. Угол при вершине этого треугольника равен 60°, следовательно, углы при основании равны
— равнобедренный. Угол при вершине этого треугольника равен 60°, следовательно, углы при основании равны 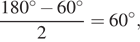 значит, треугольник
значит, треугольник 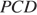 — равносторонний. Угол
— равносторонний. Угол 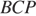 равен
равен  Аналогично получаем, что треугольник
Аналогично получаем, что треугольник 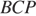 — равносторонний. Найдём угол
— равносторонний. Найдём угол 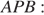
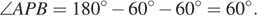 Аналогично двум предыдущим треугольникам получаем, что треугольник
Аналогично двум предыдущим треугольникам получаем, что треугольник 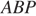 — равносторонний. Получили, что площадь трапеции равна сумме площадей трёх равных равносторонних треугольников:
— равносторонний. Получили, что площадь трапеции равна сумме площадей трёх равных равносторонних треугольников:
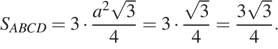
Ответ: 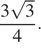
Критерии проверки:
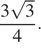
24. Задание 24

В окружности с центром 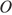 проведены две равные хорды
проведены две равные хорды  и
и 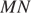 . На эти хорды опущены перпендикуляры
. На эти хорды опущены перпендикуляры 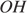 и
и 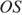 . Докажите, что
. Докажите, что 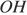 и
и 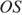 равны.
равны.
Решение.
Проведем ОK, ON, OL, OM — радиусы. Треугольники KOL и MON равны по трем сторонам, тогда высоты OH и OS также равны как элементы равных треугольников. Что и требовалось доказать.
Критерии проверки:
25. Задание 25
В треугольнике 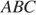 биссектриса угла
биссектриса угла 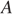 делит высоту, проведённую из вершины
делит высоту, проведённую из вершины 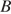 , в отношении
, в отношении 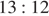 , считая от точки
, считая от точки 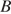 . Найдите радиус окружности, описанной около треугольника
. Найдите радиус окружности, описанной около треугольника 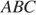 , если
, если  .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|