Контакты

Случайная статья

Многочлен и его стандартный вид. Сложение и вычитание многочленов.

Билет № 5

1) Многочлен и его стандартный вид. Сложение и вычитание многочленов.

Многочлен и его стандартный вид.

Опр.: Многочленом называют алгебраическую сумму одночленов.Пример: 2x-y+1

Слагаемые (одночлены), из которых состоит многочлен, называют членами многочлена.

Если многочлен состоит из двух слагаемых, то его называют двучлен.Пример: ax²+a

Если многочлен состоит из трёх слагаемых, то его называют трехчлен.

Пример: аx²+x - 3

Стандартный вид многочлена.

Алгоритм:

1. Все члены многочлена записать в стандартном виде.

2. Привести подобные слагаемые.

Пример:2x3xy²- 7x³2x - 3x⁴+2y⁴+5x²y²- 2xy4y²=6x²y²-14x⁴- 3x⁴+2y⁴+5x²y²-8xy³=11x²y²-17x⁴+2y⁴- 8xy³.

Опр.: Степенью многочлена называют наибольшую из степеней входящих в него одночленов. Пример: 2a²-3b+abc-d²имеет третью степень (a¹ b ¹c¹ 1+1+1=3),

4x⁴yz+2x²y³-xz⁴+3x²y²имеет шестую степень(4x⁴y ¹z ¹ 4+1+1=6).

Сложение многочленов.(a+b)+(c+d)= a+b+c+d

Правило: Если перед скобкой стоит знак «+», то скобки опускаем, а знаки многочлена не меняем.

Пример: (5x²+7x-9)+(-3x²-6x+8)=5x²+7x - 9- 3x²- 6x+8=2x²+x-1.

Вычитание многочленов.(a+b)- (c+d)= a+b - c- d

Правило: Если перед скобкой стоит знак «-», то скобки опускаем, а знаки многочлена меняемна противоположные.

Пример: (x³+5x² – x+8) – (x³+7x-1)= x³+5x² – x+8 – x³- 7x+1=5x²- 8x+9.

2) Теорема о соотношениях между сторонами и углами треугольника.

Теорема 1:

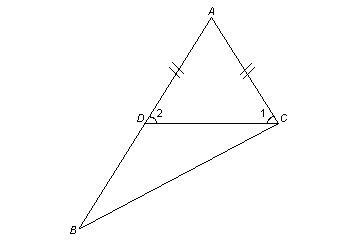В треугольнике против большей стороны лежит больший угол.

Дано: .

АВ больше АС (и ВС).

Доказать: .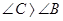

Доказательство:

I) Дополнительное построение: AD = AC, DC.

II) 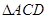- равнобедренный, тогда по свойству равнобедренного треугольника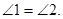

III) AD < AB, т.к. точка D лежит между точками А и В. Тогда .

IV) 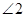- внешний угол . Тогда по теореме о внешнем угле треугольника

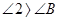(т.к. ).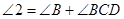

V) Из доказанного во II, III, IV получим , , .

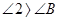Тогда .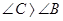

Что и требовалось доказать.

Теорема2:

В треугольнике против большего угла лежит большая сторона.

Дано: , .

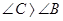Доказать: АВ > AC.

Доказательство:

Будем доказывать методом от противного.

I) Предположим, что АВ не больше АС.

Тогда АВ = АС или АВ < АС.

II) Если АВ = АС, то - равнобедренный. Тогда . А это противоречит условию.

III) Если АВ < АС, то по теореме 1 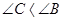. А это противоречит условию.

IV) Наше предположение неверно. Значит, АВ > AC.

Что и требовалось доказать.

Следствие:

В прямоугольном треугольнике гипотенуза больше катета.

Дано: ,

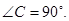
Доказать: АВ > AC.

Доказательство:

I) (прямой угол всегда больше острого угла). Тогда по теореме 2 АВ > AC.

II) Аналогично АВ > ВС.

Что и требовалось доказать.

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.