Линейное уравнение с одной переменной

Билет № 11

1) Линейное уравнение с одной переменной. Количество корней линейного уравнения.

Линейное уравнение с одной переменной

Опр: Линейным уравнением с одной переменой называется уравнение вида ax=b, где а и b–числа, а х - переменная.

Например: 3x=6; -4x=0,2.

P.S. Уравнение , которое можно привести к виду ax=b, так же называется линейным уравнением с одной переменной.

3(x -2)+5(x -7)=8

3x-6+5x-35=8

8x-41=8

8x=49

Сколько корней может иметь линейное уравнение с одной переменной?

1 корень: ax=b a≠0, x=b:a Нет корней: a=0, b≠0 Бесчисленное множество корней: a=0, b=0.

4(x+3)=3-x 4x+12=3-x 5x=-9 x=-9:5 x=-1.8 Ответ: x=-1.8 2x+5=2(x+6) 2x+5=2x+12 2x-2x=7 0x=7 Корней нет Ответ: корней нет 3(x+2)+x=6+4x 3x+6+x=6+4x 4x-4x=6-6 0x=0 x – любое число Ответ: x – любое число

2) Признаки равенства треугольников. Доказательство II признака равенства треугольников.

Опр. Треугольником называется геометрическая фигура, состоящая 3-х точек, не лежащих на одной прямой, и 3-х отрезков, соединяющих эти точки.

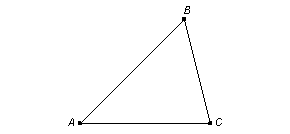
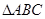
А, В, С – вершины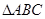

АВ, ВС, АС – стороны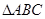

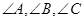– углы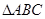

У любого треугольника 6 элементов: 3 стороны и 3 угла.

Опр. Периметром треугольника называется сумма длин 3-х сторон треугольника.

Опр. Два треугольника называются равными, если при наложении друг на друга они полностью совпадают.

Первый признак равенства треугольников

Теорема:

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Второй признак равенства треугольников.

Теорема:

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

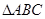Дано: и ,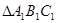

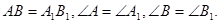
Доказать: .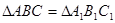

Доказательство:

1) Мысленно наложим 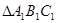на 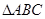так, чтобы вершина А₁ совпала с вершиной А, луч А₁В₁ пошел по лучу АВ, а вершины С и С₁ оказались по одну сторону от АВ.

2) По условию 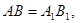тогда при наложении совместятся вершины В и В₁.

3) По условию 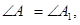тогда луч А₁С₁ пойдет по лучу АС.

4) По условию 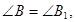тогда луч В₁С₁ пойдет по лучу ВС.

5) Так как совпадут лучи АС и А₁С₁, ВС и В₁С₁, то совпадут и точки их пересечения С и С₁.

6) Итак, треугольники при наложении полностью совместились, значит, .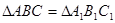

Что и требовалось доказать.

Третий признак равенства треугольников.

Теорема:

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.