Если перед скобкой ставится знак «+», то члены, которые заключаются в скобки, записываются с теми же знаками.

Билет № 6

1. Заключение многочлена в скобки. Умножение многочлена на одночлен. Вынесение общего множителя за скобки.

Заключение многочлена в скобки.

1)Если перед скобкой ставится знак «+», то члены, которые заключаются в скобки, записываются с теми же знаками.

Пример: 3x-2y+b= 3x+(-2y+b).

2) Если перед скобкой ставится знак «-», то члены, которые заключаются в скобки, записываются с противоположными знаками.

Пример:3x-2y+b=3x – (2y-b).

Умножение многочлена на одночлен.a(в+с)=ав+ас

Правило: Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый член многочлена и получившиеся произведения сложить.

Пример:-3a²(4a³-a-1)= -12a⁵+3a³+3a².

Выясним геометрический смысл формулы a(в+с)=ав+ас

для положительных а, в, с. а>0, b>0, c>0.

b+c

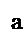
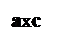
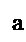
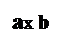Геометрический смысл: чтобы найти S прямоугольника со сторонами а и в+с, нужно найти сумму площадей прямоугольников со сторонами а и ви а и с.

a(в+с)=ав+ас

Вынесение общего множителя за скобки.

При разложении на множители способом вынесения общего множителя за скобки используют распределительные законы умножения:

ac+bc+dc=(a+b+d)c

ac-bc-dc=c(a-b-d).

Примеры:

1. 6a²b+15b²=3b(2a²+5b)

2. 3a²(b-c)+7(b-c)=(b-c)(3a²+7)

3. 6a⁴-3a³=3a³(2a -1)

4. 5a⁴ – 10a³+15a⁵=5a³(a-2+3a²)

5. 2x(x-2)+5(x-2)²=(x-2)(2x+5(x-2))=(x-2)(7x-10)

2) Теорема о внешнем угле треугольника.

Теорема о внешнем угле треугольника

Теорема:

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

Дано: .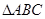

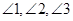- внутренние углы .

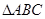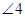- внешний угол .

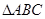Доказать: .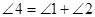

Доказательство:

I) 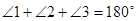(по теореме о сумме углов треугольника).

Тогда .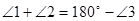

II) 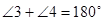(т.к. смежные углы).

Тогда .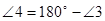

III) 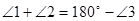(из пункта I).

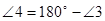(из пункта II).

Тогда 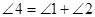(если правые части равенств равны, то равны и левые).

Что и требовалось доказать.

P.S.

1) Если медиана треугольника равна половине стороны, к которой она проведена, то этот треугольник прямоугольный.

2) Биссектриса внешнего угла при вершине равнобедренного треугольника, противолежащей основанию, параллельна основанию.

3) Если биссектриса внешнего угла треугольника параллельна стороне треугольника, то треугольник равнобедренный.