Хелпикс

Главная

Контакты

Случайная статья



Билет № 10. ax+by+c=0 является прямая.. Признаки параллельности прямых.. Доказательство III признака



Билет № 10

1) Линейное уравнение с двумя переменными. График линейного уравнения с двумя переменными.

Опр.Уравнение вида ax+by=c (ax+by+c=0)называется линейным уравнением с двумя переменными, где а, b, с – некоторые числа, а x, y- переменные.

Примеры:

1) x-y=5, a=1, b= -1, c=5   - линейное

2) x2 – y2=16        - не линейное

3) -x+2y=3, a=-1, b=2, c=3 - линейное

4) xy+x=5 - не линейное

5) x2+2y=9 - не линейное

6) 2x+0.3y-2=0, a=2, b=0.3, c=2 - линейное

Опр.Решением уравнения с двумя переменными называется пара чисел, обращающая уравнение в верное числовое равенство.

Пример:

x-y = 5

(6;1), (5.2;0.2). Всегда имеет бесчисленное множество решений.

Построим график линейного уравнения.

5x-y=10

1) x=0, 5∙0 - y=10, y=-10    (0;-10)

2) y=0, 5x - 0 =10, 5x=10, x=2 (2;0)

Вывод: Графиком любого линейного уравнения

ax+by+c=0 является прямая.

Для построения прямой достаточно двух точек.

P. S.

 1) 0x+0y=0,a=0, b=0,c=0 – вся координатная плоскость.

2) 0x+0y=c, (c≠0) – нет решений.

3) 0x+by=c,  y=c:b

Привести пример построения прямой!!!


 

3) Признаки параллельности прямых.

Доказательство III признака

Определение параллельных прямых

Опр. Две прямые на плоскости называются параллельными, если они не пересекаются.

 

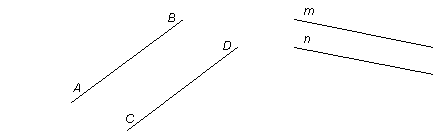
                             АВ || CD                            m || n

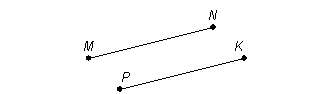Опр. Параллельными отрезками называются отрезки, лежащие на параллельных прямых.

 

MN || PK

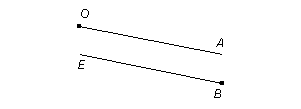Опр. Параллельными лучами называются лучи, лежащие на параллельных прямых.

 

ОА || ВЕ

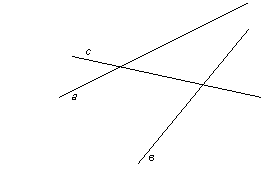Опр. Прямая с называется секущей по отношению к прямым а и в, если она пересекает их в двух точках.

Прямые а, в, с.

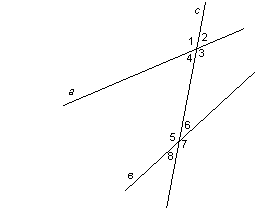Прямая с – секущая по отношению к прямым а и в.

Внутренние накрест лежащие углы: , .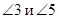

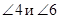Внутренние односторонние углы: , .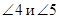

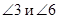Соответственные углы: , , .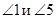

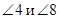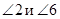
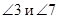Внешние накрест лежащие углы: , .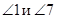

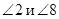Внешние односторонние углы: , .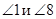

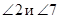I признак параллельности двух прямых

Теорема:

Если при пересечении двух прямых секущей внутренние накрест лежащие углы равны, то прямые параллельны.

II признак параллельности двух прямых

Теорема:

Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

.

III признак параллельности двух прямых

Теорема:

Если при пересечении двух прямых секущей сумма внутренних односторонних углов равна 180°, то прямые параллельны.

Дано: прямые а, в и с – секущая. 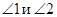 - односторонние углы, .

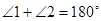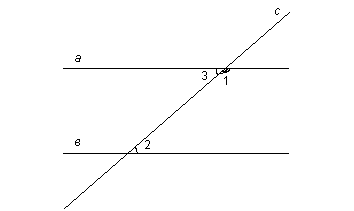Доказать: а || в

Доказательство:

1) 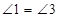- смежные углы, тогда по свойству смежных углов 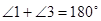. Отсюда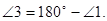

2) 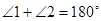 (по условию).

Тогда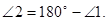

3)

      

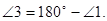
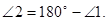
Тогда 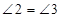(если правые части равенств равны, то равны и левые).

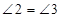- накрест лежащие углы при прямых а и в, секущей с.

Тогда а || в по первому признаку параллельности прямых.                         Что и требовалось доказать.
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.