Вариант 1. Критерий оценивания. задания

Вариант 1

1.Дана развертка многогранника:

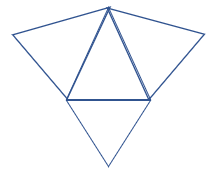
Изобразите многогранник по данной развертке и определите его вид

2.Найдите диагональ прямоугольного параллелепипеда по трем его измерениям: 8, , .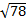

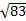3.Все боковые ребра треугольной пирамиды составляют с плоскостью основания угол 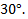Найдите высоту пирамиды, если стороны основания равны: 36 м, 29 м, 25 м.

4.В основании прямой призмы 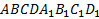лежит прямоугольник со сторонами 8 и 15 см. Диагональ 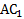составляет со стороной AD угол .

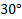Найдите:

А) высоту призмы

В) площадь сечения призмы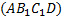

С) площадь боковой поверхности

D) площадь полной поверхности

Критерий оценивания

№

задания

Дескриптор

Балл

Обучающийся

Распознаёт развёртку многогранника, определяет вид и изображает

многогранник

изображает многогранник по данной развёртке;

определяет вид многогранника;

Применяет свойства прямоугольного

параллелепипеда

использует свойства прямоугольного параллелепипеда;

находит диагональ прямоугольного параллелепипеда;

Находит элементы

многогранников (пирамиды)

Выполняет чертеж

применяет свойство высоты, опущенной в центр описанной окружности;

находит площадь основания пирамиды;

находит радиус описанной окружности;

вычисляет высоту пирамиды;

Использует формулы площади боковой и полной поверхности призмы при решении задач

4 a

выполняет чертеж;

находит площадь основания призмы;

применяет теорему о трёх перпендикулярах;

находит боковое ребро прямой призмы (высоту);

Находит площадь сечения

находит площадь боковой поверхности;

4 b

вычисляет полную поверхность прямой призмы.

Итого: