- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вариант 1. Критерий оценивания. задания
Вариант 1
2.Точка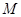 
лежит вне плоскости параллелограмма АВСD.
А) Докажите, что средние линии треугольников МАD и МВС параллельны.
В)Площадь параллелограмма АВСD равна 84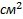 
. Высота, проведенная из вершины В на сторону AD равна 6 см. Найдите длины средних линий треугольников МАD и МВС
3. Точки А и В принадлежат различным перпендикулярным плоскостям. АС и ВD – перпендикуляры, опущенные из данных точек на прямую пересечения плоскостей.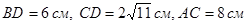 
. Найдите длину АВ
4. Через точку О, лежащую между параллельными плоскостями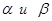 
, проведены прямые 
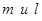. Прямая 
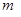пересекает плоскости 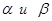в точках А и В соответственно, а прямая 
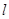– в точках С и D соответственно. 
. Найдите длину отрезка АС, выполнив рисунок
Критерий оценивания
№ задания
Балл
Орпеделяет взаимное расположение прямых в пространстве
Применяет свойства параллельных прямых
2(А)
2(В)
Применяет признак и свойства перпендикулярности плоскостей
Применяет признак и свойства параллельности плоскостей
Итого: