Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

Упражнение 5. Критерий Найквиста

Упражнение 5

     Критерий Найквиста

Варианты заданий.

№	Передаточная функция	Параметры
		T1=1с; T2=0.3с; T3=0.05с; K=20;
		T1=1с; T2=0.4с; T3=0.1с; T4=0.02с; K=35;
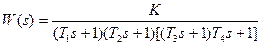
		T1=1с; T2=0.3с; T3=0.2с; T4=0.05с; K=39;
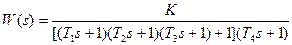
		T1=0.1с; T2=0.2с; T3=0.5с; T4=0.1с; K=100;
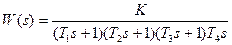
		T1=0.05с; T2=0.15с; T3=0.15с; T4=0.8с; K=10;
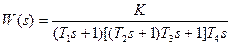
		T1=0.05с; T2=0.15с; T3=0.15с; T4=0.8с; K=10;
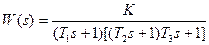
		T1=0.5с; T2=0.1с; T3=1.0с; K=15;
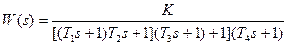
		T1=0.4с; T2=0.2с; T3=0.4с; T4=8с; K=200;
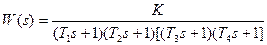
		T1=0.05с; T2=0.1с; T3=0.2с; T4=0.6с; K=20;
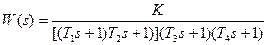
		T1=0.044с; T2=0.133с; T3=0.12с; T4=0.7c; K=25;
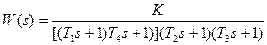
		T1=0.1с; T2=0.3с; T3=1с; T4=0.17с; K=30;
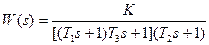
		T1=0.094с; T2=0.44с; T3=0.1с; K=16;
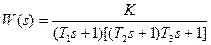
		T1=0.2с; T2=0.03с; T3=0.04с; K=54;
		T1=0.14с; T2=0.002с; T3=0.03с; K=7.5;
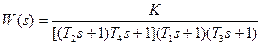
		T1=0.03с; T2=0.2с; T3=0.05с; T4=0.02с; K=10;
		T1=1с; T2=0.3с; T3=0.05с; K=20;
		T1=1с; T2=0.4с; T3=0.1с; T4=0.02с; K=35;
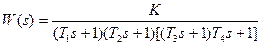
		T1=1с; T2=0.3с; T3=0.2с; T4=0.05с; K=39
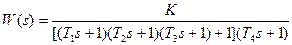
		T1=0.1с; T2=0.2с; T3=0.5с; T4=0.1с; K=100;
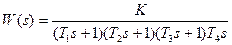
		T1=0.05с; T2=0.1с; T3=0.2с; T4=0.6с; K=20;
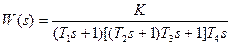
		T1=0.05с; T2=0.15с; T3=0.15с;   T4=0.8с; K=10;
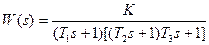
		T1=0.5с; T2=0.1с; T3=1.0с; K=15;
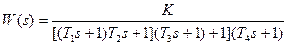
		T1=0.4с; T2=0.2с; T3=0.4с; T4=8с; K=200;
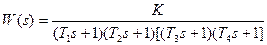
		T1=0.05с; T2=0.1с; T3=0.2с; T4=0.6с; K=20;
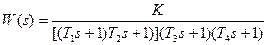
		T1=0.044с; T2=0.133с; T3=0.12с; T4=0.7c; K=40;
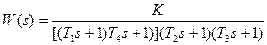
		T1=0.1с; T2=0.3с; T3=1с; T4=0.17с; K=30;
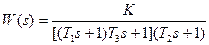
		T1=0.094с; T2=0.44с; T3=0.1с; K=16;
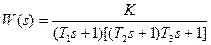
		T1=0.2с; T2=0.03с; T3=0.04с; K=54;
		T1=0.14с; T2=0.002с; T3=0.03с; K=7.5;
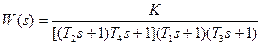
		T1=0.03с; T2=0.2с; T3=0.05с; T4=0.02с; K=10

                                        Порядок выполнения задания.

1. Найти действительную и мнимую части передаточной функции разомкнутой системы.

2. Построить амплитудно-частотную характеристику разомкнутой системы.

3. Определить состояние системы (устойчива, не устойчива, на грани устойчивости) для заданного значения коэффициента К.

4. Найти остальные два значения коэффициента К (методом подбора) при которых система будет находиться в двух других состояниях, построив амплитудно - частотные характеристики.

 5. Найти передаточную функцию замкнутой системы.

6. Для найденных значений коэффициента К построить амплитудно-частотные характеристики замкнутой системы и определить устойчивость

замкнутой системы во всех трех случаях.

7. Определить запасы устойчивости по модулю и фазе для устойчивой системы, используя функцию “margin” пакета MATLAB.

Примеры построения амплитудно-частотных характеристик. На рисунках точка с координатами (-1, j0) обозначена знаком (+).

Система неустойчива (рис. 1), так как годограф Найквиста охватывает точку с координатами (-1, j0). К = …

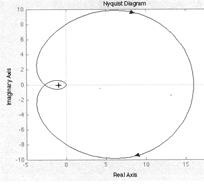
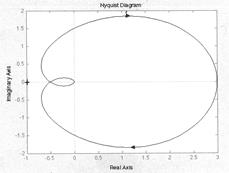
       Рис.1 Неустойчивая система                Рис.2 Устойчивая система

Система устойчива (рис.2), так как годограф Найквиста не охватывает точку с координатами (-1, j0). К = …

Система на грани устойчивости (рис.3, а, б), так как годограф Найквиста проходит через точку с координатами (-1, j0). К = …           

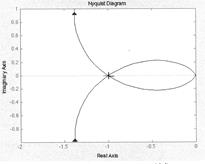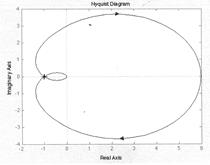                                       а)                                                                     б)

                 Общий вид годографа             Начальный участок годографа

                                       Рис.3 Система на грани устойчивости