Контакты

Случайная статья

Линеаризация функции нескольких переменных

Линеаризация функции нескольких переменных

дано:

· функция 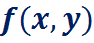и базовая точка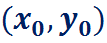

получить:

· простую приближенную формулу для 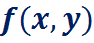в окрестности базовой точки: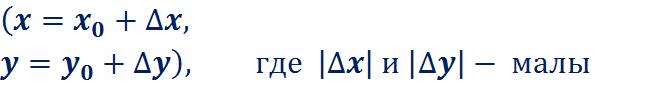

Решение:

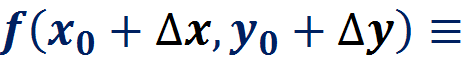
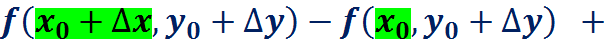
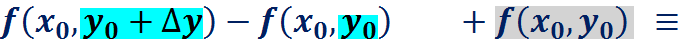
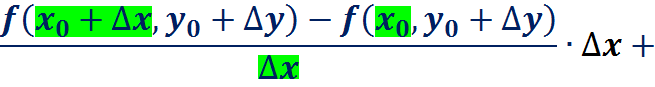
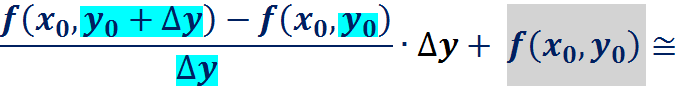
Пример:

===========================================

===========================================

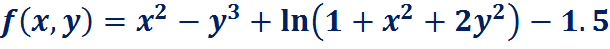
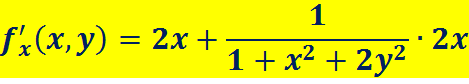
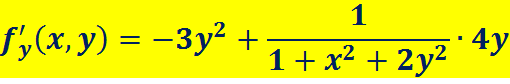
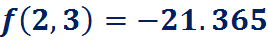
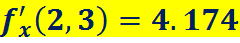
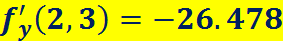
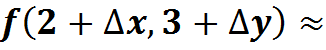
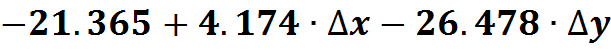
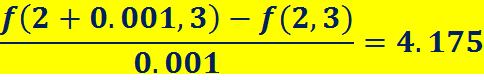
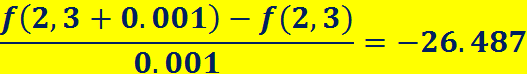
Решение системы нелинейных алгебраических уравнений:                                      метод Ньютона-Рафсона



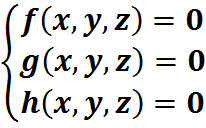
Зададим начальное приближение: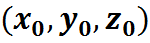

Решение будем искать в виде:



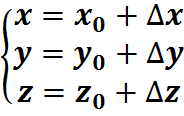
Проведем линеаризацию уравнений:

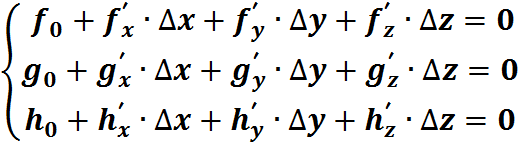
Здесь: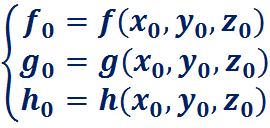

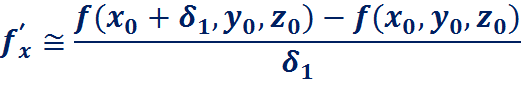
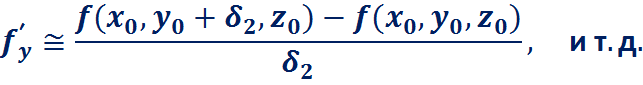
Для расчета поправок 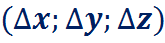получим систему линейных алгебраических уравнений:

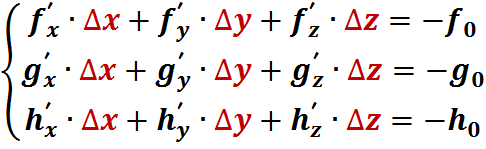
В линейной алгебре такие уравнения принято записывать следующим образом:

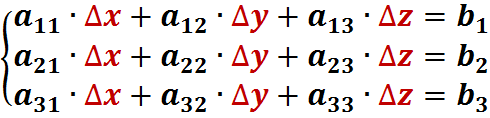
Решение имеет вид:

; ;

; ;

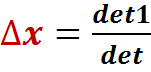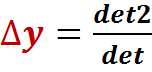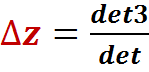
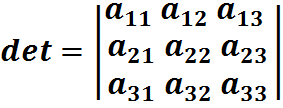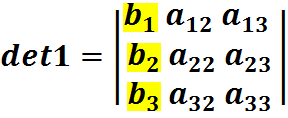; и т.д.

Вычислим новое приближение по формулам:

; ;

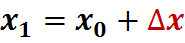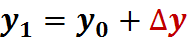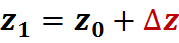
и повторим все сначала.

==============================================================

ВАР. 2 (два уравнения с двумя неизвестными)

Function r(x, y)

r = (x + 0.7 * y) ^ 2 + (y - 2 * x) ^ 2 - 1.17

End Function

Function s(x, y)

s = Atn(x) + Atn(y) + Atn(x - y) - 0.58

End Function

x₀ = 1 y₀ = 1

===============================================================

ВАР. 3 (три уравнения с тремя неизвестными)

Function f(x, y, z)

f = x ^ 2 - y ^ 3 + Log (1 + x ^ 2 + y ^ 2) - 1.44

End Function

Function g(x, y, z)

g = x + 2 * y - Exp (z - x) - 1.36

End Function

Function h(x, y, z)

h = Atn(y + 3 * z - x) - 0.03

End Function

x0 = 2 y0 = 3 z0 = 0

===============================================================

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.