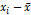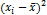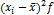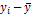Решение. Таблица 21 - Исходные данные

Задача 1.3Определить:

Вариант	Условие варианта
3,10	среднюю арифметическую, моду и медиану
	коэффициент вариации

По данным соответствующего варианта (таблица 3)

Таблица 3 - Исходные данные

Вариант	Показатели	Значения
	Удельный вес жилой	38,1	35,1	30,8	22,2	12,9	12,6	24,4	28,8
	площади, приходящейся	34,5	34,1	28,8	21,8	20,8	12,8	22,2	30,4
	на одного человека в	33,9	37,2	30,4	32,4	20,3	20,8	26,4	34,6
	общей площади	35,1	33,8		33,4	38,4	24,6	23,8	35,8
	квартир, м²	34,5	34,0		35,6	34,6	22,0	26,4	36,0

выполнитьследующее задание и дать характеристику распределения.

Вариант	Условие варианта
	Построить равноинтервальный ряд распределения ,вычертить гистограмму;
	построить ряд распределения; начертить полигон распределения

Удельный вес жилой площади, приходящейся на одного человека, м²

Решение

Чтобы произвести группировку данных, необходимо ранжировать данные.

12,6	26,4	34,6
12,8	26,4	34,6
12,9	28,8	35,1
20,3	28,8	35,1
20,8	30,4	35,6
20,8	30,4	35,8
21,8	30,8
	32,4	37,2
22,2	33,4	38,1
22,2	33,8	38,4
23,8	33,9
24,4
24,6	34,1
	34,5
	34,5

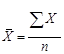- средняя арифметическая простая.

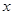- отдельное значение

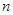- единиц в совокупности.

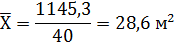
Средний удельный вес жилой площади, приходящейся на одного человека в общей площади квартир 28,6 м².

Модой (Мо) называют значение признака, которое встречается наиболее часто у единиц совокупности. В данном примере мода отсутствует, так как имеются несколько показателей с одинаковым значением.

Медиана (Ме) - это величина, которая соответствует варианту, находящемуся в середине ранжированного ряда.

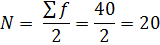
Для ранжированного ряда с четным числом индивидуальных величин медианой будет средняя арифметическая величина, которая рассчитывается из двух смежных величин. Значит по накопленной частоте находим среднее значение показателей с 20 – 21-м номерами. Ме = (30,4+30,4)/2 = 30,4

x_i	Кол-во, f_i	x_i * f_i	Накопленная частота, S	\|x - x_ср\|*f_i	(x - x_ср)²*f_i	Частота, f_i/f
12.6		12.6		16.033	257.041	0.025
12.8		12.8		15.833	250.668	0.025
12.9		12.9		15.733	247.512	0.025
20.3		20.3		8.333	69.431	0.025
20.8		41.6		15.665	122.696	0.05
21.8		21.8		6.833	46.683	0.025
				6.633	43.99	0.025
22.2		44.4		12.865	82.754	0.05
23.8		23.8		4.833	23.353	0.025
24.4		24.4		4.233	17.914	0.025
24.6		24.6		4.033	16.261	0.025
				3.633	13.195	0.025
				2.633	6.93	0.025
26.4		52.8		4.465	9.968	0.05
28.8		57.6		0.335	0.0561	0.05
30.4		60.8		3.535	6.248	0.05
30.8		30.8		2.168	4.698	0.025
32.4		32.4		3.768	14.194	0.025
33.4		33.4		4.768	22.729	0.025
33.8		33.8		5.168	26.703	0.025
33.9		33.9		5.268	27.747	0.025
				5.368	28.81	0.025
34.1		34.1		5.468	29.894	0.025
34.5				11.735	68.855	0.05
34.6		69.2		11.935	71.222	0.05
35.1		70.2		12.935	83.657	0.05
35.6		35.6		6.968	48.546	0.025
35.8		35.8		7.168	51.373	0.025
				7.368	54.28	0.025
37.2		37.2		8.568	73.402	0.025
38.1		38.1		9.468	89.634	0.025
38.4		38.4		9.768	95.404	0.025
Итого		1145.3		243.505	2005.848

Коэффициент вариации

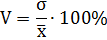
Среднее квадратичное отклонение;

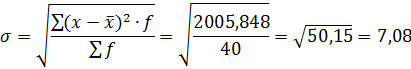
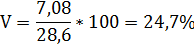
Поскольку v ≤ 30%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять.

Для построения полигона распределения (рис 1) по оси абсцисс (X) откладываем количественные значения варьирующего признака — варианты, а по оси ординат — частоты или частости.

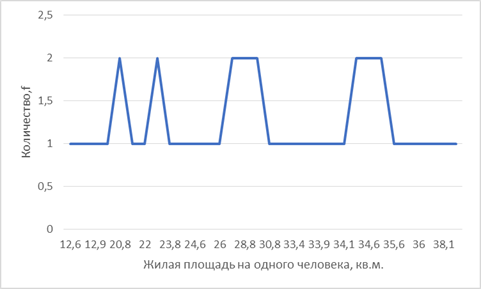
Рис. 1 Полигон распределения

Задача 1.13 При повторной выборке произведено выборочное измерение выработки на земляных работах у 144 рабочих. В результате этого обследования средняя выработка по выборочным данным определена в 5,25 м³ на одного рабочего, а средний квадрат отклонения оказался равным 2,25.

Определите: 1) точность выборочного наблюдения, т.е. размер средней ошибки выборки и пределы, где находятся размеры средней выработки у всех рабочих с вероятностью 0,683 ; 0,954 и 0,997; 2) какова должна быть численность выборки, чтобы размер ошибки выборки не превышал 0,05 м³; 3) какова будет численность выборки, если уменьшить вдвое точность выборки, т.е. размер ошибки выборки не должен превышать 0,1 м³; 4) какова должна быть численность выборки, если с вероятностью в 0,954гарантировать,что размер ошибки выборки не будет превышать 0,1м³?

1) Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности.

Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений: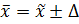

Вычислим предельную ошибку по формуле:

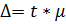
Средняя ошибка выборки:

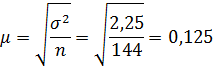
с вероятностью, равной 0,683 (t=1)

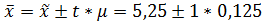
можно заявить, что средняя выработка у всех рабочих находится в пределах от 5,125 м3 (5,25-0,125) до 5,375 м3 (5,25+0,125),

с вероятностью, равной 0,954 (t=2), средняя выработка у всех рабочих будут находиться в пределах от 5 м3 (5,25-(2*0,125)) до 5,5 м3 (5,25+(2*0,125)) и с вероятностью, равной 0,997 (t=3), средняя выработка у всех рабочих будут находиться в пределах от 4,875м3 (5,25-(3*0,125)) до 5, 5,625 м3 (5,25+(3*0,125))

2) Для определения численности выборки (n) воспользуемся формулой:

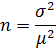
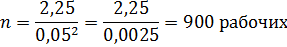
3) Численность выборки определим по той же формуле, по которой определили численности рабочих.

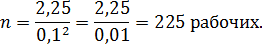
4) В этом случае для определения численности выборки, т.е. количества рабочих, которые должны попасть в выборку, используем формулу

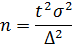
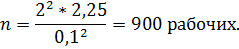
Задача 1.15Определитьвид корреляционной зависимости. Рассчитатьпараметры уравнения регрессии и определитьтесноту связи.

Вариант	Условие варианта
	между реализованной продукцией и балансовой прибылью(таблица8)

Таблица 8 - Исходные данные

Объем реализован-	Балансовая прибыль, тыс. р.
ной продукции, млн р.	250-360	320-350	350-400	400-500	550-600
1,7-3,7			-	-	-
3,7-5,7				-	-
5,7-7,7	-				-
7,7-9,7	-	-
9,7-11,7	-	-	-
11,7-13,7	-	-	-	-

Решение

Объем реализованной продукции - фактор, балансовая прибыль - результат

По интервальным рядам распределения определим середину интервала (1,7+3,7)/2 = 2,7 (250+360) /2 = 305

Для определения тесноты парной связи и формы связи для групп, полученных в результате комбинационной группировки, с составляю корреляционную таблицу

Объем реализованной продукции, млн р.	Середина интервала	Балансовая прибыль, тыс. р.					f
Объем реализованной продукции, млн р.	Середина интервала	250-360	320-350	350-400	400-500	550-600

1,7-3,7	2,7			-	-	-		-3,76	14,1376	141,37
3,7-5,7	4,7				-	-		-1,76	3,0976	43,366
5,7-7,7	6,7	-				-		0,24	0,0576	0,57
7,7-9,7	8,7	-	-					2,24	5,0176	40,14
9,7-11,7	10,7	-	-	-				4,24	17,9776	71,91
11,7-13,7	12,7	-	-	-	-			6,24	38,9376	155,75
f										453,12
		-72,7	-42,7	-2,7	72,3	197,3
		5285,29	1823,29	7,29	5227,29	38927,3
		84564,64	23702,77	65,61	26136,45	272491,0	406960,5			11752,4

Вычислим средние

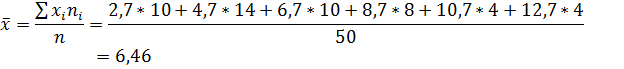
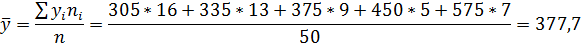
Как средние величины признаков, так и все суммы, входящие в расчет параметров корреляции, при группировке взвешиваются на соответствующие частоты.

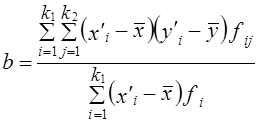
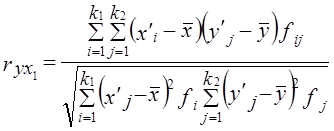
где x'i, yj. - середины интервалов i-й категории х и j-й категории y;

fi - частота i-го значения х;

fj - частота j-го значения у;

fij - частота совместного появления i-го значения х и j-гo значения у (это числа в клетках «корреляционной решетки»).

Взвешенные суммы квадратов отклонений подсчитаны и приведены в последней графе и в последней строке таблицы. Для вычисления числителя в формулах необходимо умножить отклонения по обоим признакам (с учетом их знаков) на частоты совместного распределения и сложить все 14 произведений:

(-72,7)*(-3,76)*7 – 42,7*(-3,76)*3-72,7*(-1,76)*9-42,7*(-1,76)*4-2,7*(-1,76)*1 – 42,7*0,24*6 – 2,7*0,24*3 + 72,3*0,24*1 – 2,7*2,24*5+72,3*2,24*2+197,3*2,24*1 +72,3*4,24*2+197*4,24*2+197,3*6,24*4 = 11752,4

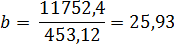
Это означает, что в среднем с увеличением объема реализации продукции на 1 млн. руб. балансовая прибыль увеличивается на 25,93 тыс. руб.)

Определяем параметр а

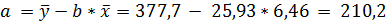
Уравнение имеет вид:

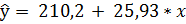
Коэффициент корреляции согласно r составляет:

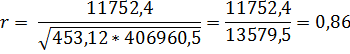
Связь прямая и тесная.

Задача 1.16 Согласно своему варианту , указанному в нижеприведенной таблице, выполните требуемые расчеты.

Вариант	Исходные данные о ( об )	Номер
	объеме промышленной продукции ( ОПП )	Таблица 11

Таблица 11 - Исходные данные

Месяцы
РТО,млрд р	68,6	64,3	67,8	69,4	68,4	68,1	69,0	71,5	74,6	74,9	76,5	89,5
ОПП,млрдр	119,8	122,9	134,1	130,7	125,7	128,0	130,1	132,2	132,7	140,9	136,3	142,9

Определитев соответствии с заданием (“+”) согласно варианту:

Название показателей	Варианты

1. Средний уровень ряда		+		+			+	+		+
2. Абсолютный прирост 2.1.Базисный 2.2.Цепной				+			+		+	+ +
3. Средний абсолютный прирост				+			+		+
4. Темпы роста 4.1. Базисный 4.2. Цепной 4.3. Средний	+ + +	+ +	+ + +		+ + +	+ + +	+	+ +	+	+
5. Темпы прироста 5.1. Базисный 5.2. Цепной		+	+	+	+		+		+
5.3. Средний	+	+	+		+	+		+		+
6. Абсолютное значение 1 % прироста	+			+		+		+	+
7. Произвести сглаживание ряда 7.1. Методом скользящей средней - период равен четырем - период равен трем 7.2. Аналитическое	+	+	+	+	+	+	+	+	+	+

Решение

Средний уровень ряда рассчитывается по формуле:

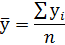
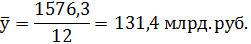
Абсолютный прирост

базисный

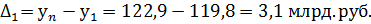
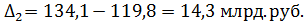
цепной

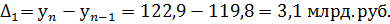
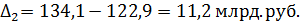
Полный расчет представлен в таблице.

Годы	ОПП, млрд. руб.	Абсолютное отклонение млрд. руб. +, -
Годы	ОПП, млрд. руб.	базисный	цепной
	119,8
	122,9	3,1	3,1
	134,1	14,3	11,2
	130,7	10,9	-3,4
	125,7	5,9	-5
		8,2	2,3
	130,1	10,3	2,1
	132,2	12,4	2,1
	132,7	12,9	0,5
	140,9	21,1	8,2
	136,3	16,5	-4,6
	142,9	23,1	6,6
Итого	1576,3		23,1

Средний темп роста

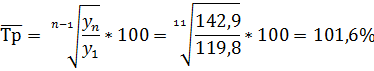
Средний темп прироста

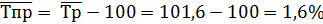
Произвести сглаживание ряда методом скользящей средней, период равен 3.

Определим трехлетние скользящие средних по формуле простой средней арифметической:

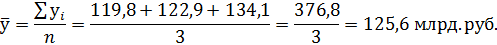
Полученное значение записываем в 2 году. Затем берем следующую трехлетнюю скользящую сумму и находим трехлетнюю скользящую среднюю: 387,7 / 3 = 129,2, полученное значение записываем в 3 году и т.д.

Годы	ОПП, млрд. руб.	Трехлетние скользящие суммы, млрд. руб.	Трехлетние скользящие средние, млрд. руб.
Годы	ОПП, млрд. руб.	Трехлетние скользящие суммы, млрд. руб.	Трехлетние скользящие средние, млрд. руб.
	119,8	-	-
	122,9	-	125,6
	134,1	376,8	129,2
	130,7	387,7	130,2
	125,7	390,5	128,1
		384,4	127,9
	130,1	383,8	130,1
	132,2	390,3	131,7
	132,7		135,3
	140,9	405,8	136,6
	136,3	409,9	140,0
	142,9	420,1	-

Скользящая средняя действительно помогла более отчетливо выявить тенденции в развитии ОПП. Объем промышленной продукции за 12 лет имеет тенденции к росту.

Задача 1.26 Определить ( таблица 21 ) индивидуальные и общий индексы производительности труда ( ПТ ) , а также экономию в затратах времени за счет ПТ. БП - базисный период; ОП - отчетный период . Сделать выводы.

Таблица 21 - Исходные данные

	Изготовлено (g ), шт.			Затрачено времени(Т)чел.-ч			ПТ(w = g / Т, t = T / q )
Фирмы	БП(g_o)	ОП(g₁)	i_g	БП (Т₀)	ОП(Т₁)	i _Т	ПТ₀	ПТ₁	i _ПТ
№1
№2
№3
Итого

Решение

Индивидуальные индекс производительности труда:

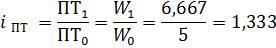
Расчет представлен в таблице.

Фирмы	Показатели производительности труда				Индивидуальные индексы
	прямые		обратные		i= W₁/W₀	i=t₀/t₀
	базисный год	отчетный год	базисный год	отчетный год
	W₀=q₀/T₀	W₁=q₁/T₁	t₀=T₀/q₀	t₁=T₁/q₁
№1		6,667	0,2	0,15	1,333	1,333
№2		2,500	0,5	0,4	1,25	1,25
№3	2,5	2,000	0,4	0,5	0,8	0,8

Общий индекс производительности труда находим, рассчитав индекс производительности труда натуральный

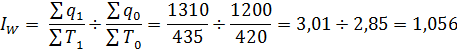
Производительность труда увеличилась на 5,6%.

Агрегатный индекс производительности труда по трудовому методу:

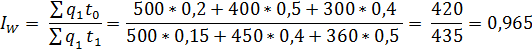
Рассчитываем экономию (увеличение) фактических затрат труда вследствие изменения (роста или снижения) его производительности

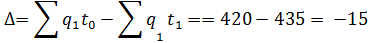
Рост производительности труда вызвал снижение трудовых затрат на производство в размере 15 чел.-час.