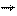Хелпикс

Главная

Контакты

Случайная статья



Прямоугольная система координат.

Стр 1 из 2Следующая ⇒


 

Тема:Прямоугольная система координат. Векторы в пространстве. Координаты вектора.

Цели урока:

1. Обучающая – сформировать понятие о прямоугольной системе координат, координатах вектора.

2. Развивающая – развитие познавательного интереса учащихся.

3. Воспитывающая – воспитание к стремлению новых знаний.

Задачи урока: Научить находить координаты вектора.

 

Ход урока

I. Приветствие. Сообщение темы и цели урока.

II. Проверка домашенего задания.

III. Изложение нового материала.

Прямоугольная система координат.

Векторы в пространстве. Координаты вектора

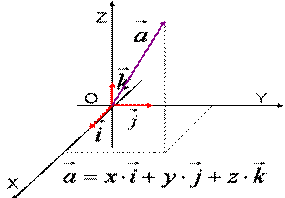
   Прямые x, y, z называются координатными осями (или осями координат),
точка их пересечения O – началом координат,
а плоскости xOy, xOz и yOz – координатными плоскостям. Точка O разбивает каждую координатную ось на две полупрямые, которые называются положительной и отрицательной полуосями.

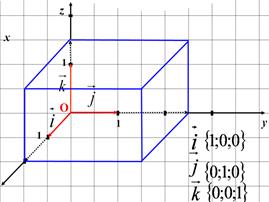
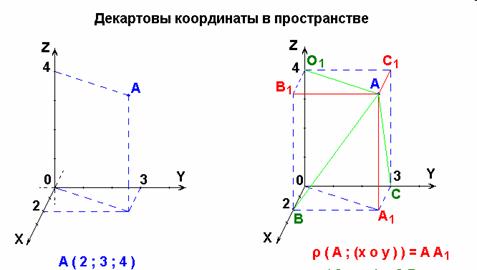
     Координатой точки A по оси x будем называть число, равное по абсолютной величине длине отрезка OAx: положительное, если точка A лежит на положительной полуоси x, и отрицательное, если она лежит на отрицательной полуоси. Аналогично можно определить координаты y и z точки A. Координаты точки A записываются в скобках рядом с названием этой точки: A (x; y; z).

 
  

    

 

Единичным вектором или ортом называется вектор, длина которого равна единице и который направлен вдоль какой-либо координатной оси. Вектора i , j , k называются координатными векторами. Любой вектор можно разложить по координатным векторам: 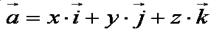             Коэффициенты разложения определяются единственным образом и называются координатами вектора  в данной системе координат.     
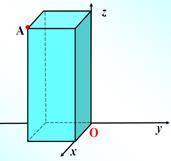
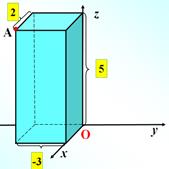
- Единичный вектор, направленный вдоль оси x, обозначается i . - Единичный вектор, направленный вдоль оси y, обозначается j . - Единичный вектор, направленный вдоль оси z, обозначается k .                                                                   

Ø Координаты нулевого вектора равны нулю.

Ø Координаты равных векторов соответственно равны.

Ø Координаты вектора суммы двух векторов равны сумме соответствующих координат этих векторов.

Ø Координаты вектора разности двух векторов равны разностям соответствующих координат этих векторов.

Ø Координаты вектора произведения данного вектора на число равны произведениям соответствующих координат этого вектора на данное число.

IV. Закрепление.(мультимедийная презентация) Решение задач по готовому чертежу

 Задача №1 Рассмотрим точку А и найдём её координаты по чертежу: Ответ: А(2; -3; 5)



Задача№2 Найти координаты точек:

Задача№3     Определите координаты векторов: ОА; ОА1; ОА2      

12Следующая ⇒
  

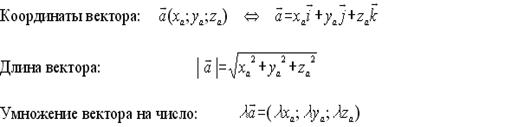
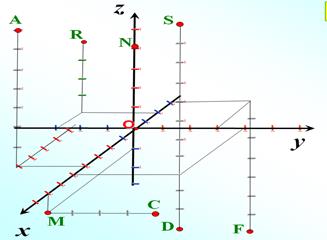© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.