Виды движения

Преобразование плоскости. Движение.

Преобразованием плоскости называется соответствие, заданное на множестве точек этой плоскости, при котором каждой точки плоскости ставится в соответствие единственная точка этой же плоскости.

Преобразования плоскости обозначаются прописными латинскими буквами R, Q …

R : X→X₁ Х₁ – образ точки Х при данном преобразовании, X – прообраз точки Х₁.

Образом фигуры F при преобразовании R множество образов точек данной фигуры при преобразовании R.

Движение

Движением называется преобразование плоскости, которое не меняет расстояние между точками. Т.е, если R – движение, и A→ A₁, B→ B₁, то AB=A₁B₁.

Свойства движения.

Движение прямую переводит в прямую, отрезок в отрезок, луч в луч.
При движении угол переходит в равный ему угол.
Движение переводит фигуру в равную ей фигуру.

Виды движения

Параллельный перенос

Параллельным переносом на вектор 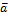называется преобразование плоскости, при котором точка A→ A₁ так, что .

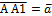Теорема. Параллельный перенос является движением.

Из теоремы можно вывести так же следующее свойство параллельного переноса: прямая, не параллельная вектору переноса, переходит в параллельную ей прямую. Если прямая параллельна вектору переноса, то она переходит в себя ( неподвижна).

Симметрия относительно точки.

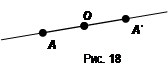
Пусть О - фиксированная точка и А - произвольная точка плоскости. Точка А' называется симметричной точке А относительно точки О, если точки А, О, А' лежат на одной прямой и ОА = ОА' (рис. 18). Точка, симметричная точке О, есть сама эта точка.

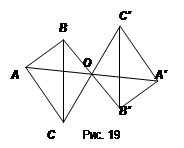
Пусть Р - данная фигура и О - фиксированная точка плоскости. Преобразование фигуры Р в фигуру Р', при котором каждая точка А фигуры Р переходит в точку А' фигуры Р', симметричную А относительно точки О, называется преобразованием симметрии относительно точки О. На рисунке 19 выполнено преобразование треугольника АВС в симметричный ему относительно точки О треугольник А'В'С'.

Если преобразование симметрии относительно точки О переводит фигуру в себя, то фигура называется центрально симметричной, а точка О - ее центром симметрии.

Например, центрально симметричными являются параллелограмм (центром симметрии в нем является точка пересечения диагоналей), окружность с центром в точке О.

При симметрии относительно точки прямая переходит в параллельную ей прямую, если она не содержит центр симметрии. Если центр симметрии принадлежит прямой, то прямая переходит в себя.

Симметрия относительно прямой.

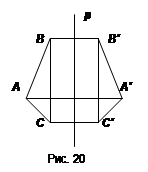Пусть р - фиксированная прямая. Тогда А' называется симметричной точке А относительно прямой р, если прямая АА' перпендикулярна прямой р и ОА' = ОА, где О - точка пересечения прямых АА' и р (рис. 20).

Если точка А лежит на прямой р, то симметричная ей точка есть сама точка А. Точка, симметричная точке А', есть точка А.

Пусть Р - данная фигура и р - фиксированная прямая. Преобразование фигуры Р в фигуру Р', при котором каждая точка А фигуры Р переходит в точку А' фигуры Р', симметрично относительно прямой р, называется преобразованием симметрии относительно прямой?. При этом фигуры Р и Р' называются симметричными относительно прямой р. На рисунке 20 изображены треугольники АВС и А'В'С', симметричные относительно прямой р.

Если преобразование симметрии относительно прямой р переводит фигуру Р в себя, то фигура называется симметричной относительно прямой р, прямая р называется осью симметрии фигуры. Например, осями симметрии прямоугольника являются прямые, проходящие через точку пересечения его диагоналей параллельно сторонам.

Поворот

Поворотом на угол a с центром в точке О называется преобразование плоскости, при котором точка A переходит в точку A₁ так, что угол AOA₁ равен а и AO=A₁O

Пример поворот вокруг точки О на 60 градусов.

Поворот является движением.