
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
a(0)=1, a(1)=2, a(k)=(4×k-2)×a(k-1)+ a(k-2); (k=2,3,…);
⇐ ПредыдущаяСтр 3 из 3
a(0)=1, a(1)=2, a(k)=(4×k-2)×a(k-1)+ a(k-2); (k=2,3,…);
b(0)=0, b(1)=1, b(k)=(4×k-2)×b(k-1)+ b(k-2); (k=2,3,…);
 при
при  .
.
7. Пусть x, y, z – целые числа. Написать рекурсивную программу, вычисляющую классическую в теории рекурсии функцию Кадью:

8. Индивидуальное задание. Решите приваленное ниже задание, используя рекурсивный алгоритм.
| № | Задание |
| 1. | В теории вычислимости важную роль играет функция Аккермана A(m,n), определенная следующим образом: 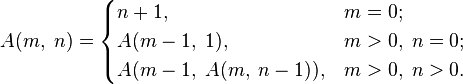 Даны два целых неотрицательных числа m и n, каждое в отдельной строке. Выведите A(m,n). Даны два целых неотрицательных числа m и n, каждое в отдельной строке. Выведите A(m,n).
|
| 2. | Дано натуральное число N. Выведите слово YES, если число N является точной степенью двойки, или слово NO в противном случае. Операцией возведения в степень пользоваться нельзя! |
| 3. | Дано натуральное число N. Вычислите сумму его цифр, используя рекурсивный алгоритм. |
| 4. | Дано натуральное число N. Выведите все его цифры по одной, в обратном порядке, разделяя их пробелами или новыми строками. Разрешена только рекурсия и целочисленная арифметика. |
| 5. | Дано натуральное число n>1. Проверьте, является ли оно простым. Программа должна вывести слово YES, если число простое и NO, если число составное. Алгоритм должен иметь сложность O(logn). Указание. Понятно, что задача сама по себе нерекурсивна, т.к. проверка числа n на простоту никак не сводится к проверке на простоту меньших чисел. Поэтому нужно сделать еще один параметр рекурсии: делитель числа, и именно по этому параметру и делать рекурсию. |
| 6. | Дано натуральное число n>1. Выведите все простые множители этого числа в порядке не убывания с учетом кратности. |
| 7. | Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Выведите первое, третье, пятое и т.д. из введенных чисел. Завершающий ноль выводить не надо. В этой задаче нельзя использовать глобальные переменные и передавать какие-либо параметры в рекурсивную функцию. Функция получает данные, считывая их с клавиатуры. Функция не возвращает значение, а сразу же выводит результат на экран. Основная программа должна состоять только из вызова этой функции. |
| 8. | Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Определите наибольшее значение числа в этой последовательности. В этой задаче нельзя использовать глобальные переменные и передавать какие-либо параметры в рекурсивную функцию. Функция получает данные, считывая их с клавиатуры. Функция возвращает единственное значение: максимум считанной последовательности. Гарантируется, что последовательность содержит хотя бы одно число (кроме нуля). |
| 9. | Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Выведите все нечетные числа из этой последовательности, сохраняя их порядок. В этой задаче нельзя использовать глобальные переменные и передавать какие-либо параметры в рекурсивную функцию. Функция получает данные, считывая их с клавиатуры. Функция не возвращает значение, а сразу же выводит результат на экран. Основная программа должна состоять только из вызова этой функции. |
| 10. | Дана монотонная последовательность, в которой каждое натуральное число k встречается ровно k раз: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4,… По данному натуральному n выведите первые n членов этой последовательности. Попробуйте обойтись только одним циклом for. |
| 11. | Реализуйте рекурсивный алгоритм вычисления последовательности n вложенных корней 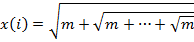 , m³0, i=1,...,n. , m³0, i=1,...,n.
|
| 12. | Даны натуральные числа k и s. Определите, сколько существует k-значных натуральных чисел, сумма цифр которых равна d. Запись натурального числа не может начинаться с цифры 0. В этой задаче можно использовать цикл для перебора всех цифр, стоящих на какой-либо позиции. |
| 13. | Реализуйте рекурсивный алгоритм вычисления суммы n первых членов ряда
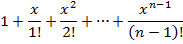
|
| 14. | Дано число n, десятичная запись которого не содержит нулей. Получите число, записанное теми же цифрами, но в противоположном порядке. |
| 15. | Составить рекурсивную программу ввода с клавиатуры последовательности чисел (окончание ввода - 0) и вывода ее на экран в обратном порядке. |
| 16. | Вывести все сочетания из n по k (  ) )
|
| 17. | Дано натуральное число. Число представлено в десятичной системе счисления. Переведите его в систему счисления с основанием 8. |
| 18. | Определите n–й член последовательности, в которой каждый следующий член равен сумме квадратов всех предыдущих. |
| 19. | Реализуйте рекурсивный алгоритм вычисления суммы n первых членов ряда
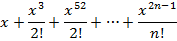
|
| 20. | Составьте программу для нахождения суммы членов арифметической прогрессии, |
| 21. | Составьте программу для нахождения n-го члена геометрической прогрессии, |
| 22. | Даны два целых числа a и b. Выведите все числа от a до b включительно, в порядке возрастания, если a < b, или в порядке убывания в противном случае. |
| 23. | Вывести все размещения из n по k ( 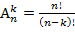 ) )
|
| 24. | Составьте программу для нахождения n-го члена ряда Фибоначчи. |
| 25. | Дано целое положительное число N. Выведите на экран все число от N до 1 (по убыванию). |
| 26. | Реализуйте рекурсивный алгоритм вычисления суммы n первых членов ряда
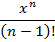
|
| 27. | Реализуйте рекурсивный алгоритм вычисления суммы n первых членов ряда
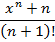
|
| 28. | Реализуйте рекурсивный алгоритм вычисления суммы n первых членов ряда
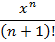
|
| 29. | Реализуйте рекурсивный алгоритм вычисления суммы n первых членов ряда
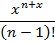
|
| 30. | Реализуйте рекурсивный алгоритм вычисления суммы n первых членов ряда
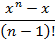
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|