
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Специальность. Вариант № Образец
Государственное автономное образовательное учреждение
среднего профессионального образования Республики Крым
«Ялтинский медицинский колледж»
Экзамен по учебной дисциплине ОУД.04МАТЕМАТИКА
Специальность
34.02.01 Сестринское дело
31.02.03 Лабораторная диагностика
Вариант № Образец
1. (1 балл) Вычислите значение выражения 
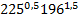 ;
;
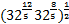 ;
;
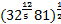
2. (1 балл) Площадь поверхности куба 108 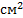 . Вычислите
. Вычислите
а) ребро куба.
б) объем куба
Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3 см. Найдите:
- боковую поверхность параллелепипеда;
- объем параллелепипеда;
- площадь всей поверхности
3. ( 1 балл) В коробке лежит 4 белых, 8 черных, 12 синих шаров. Какова вероятность того, что будет наугад вытащен синий шар.
4. ( 2 балла) Докажите тождество 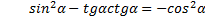
5. ( 2 балла) Решите уравнение 
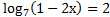
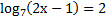
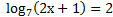
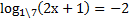
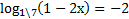
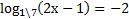
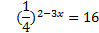
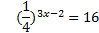
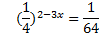
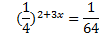
6.  ( 2 балла) Решите неравенство
( 2 балла) Решите неравенство 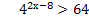 ;
;
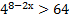
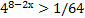
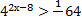 ;
;
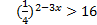
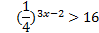
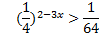
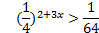
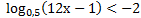
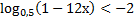
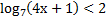
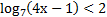
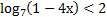
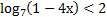
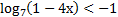
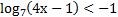
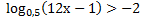
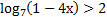
7. Используя график функции у= f(х), определите и запишите ответ: 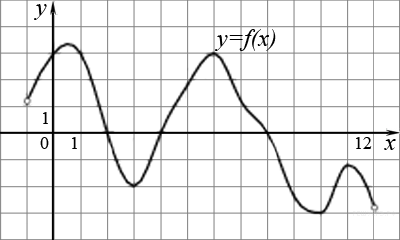
( 1 балл) наименьшее и наибольшее значение функции
( 1 балл) промежутки возрастания и убывания функции
8. ( 3 балла) Вычислить определенный интеграл 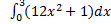
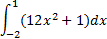
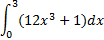
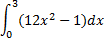
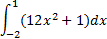
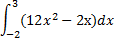
9. ( 3 балла) Найдите решение уравнения 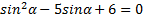
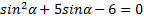
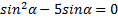
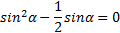
2 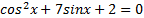
2 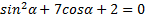
2 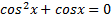
2 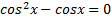
10. ( 3 балла) Высота правильной треугольной пирамиды равна 6 см, а боковое ребро – 10 см.
а) найти объем пирамиды.
б) найти площадь поверхности пирамиды.
( 3 балла) Высота правильной четырехугольной пирамиды равна 6 см, а боковое ребро – 10 см.
а) найти объем пирамиды.
б) найти площадь поверхности пирамиды.
11. Через концы отрезка АВ и его средину точку М проведены параллельные прямые, пересекающие плоскость в точках К, Р, О. Вычислить длину отрезка МО, если АК равно 3,6 дм, а ВР 4,8 дм. Рассмотреть два случая.
12. Телефонный провод длиной 15 м протянут от телефонного столба на высоте 6м к дому на высоту 20 м. Вычислить расстояние от столба к дому, если известно, что провод не провисает.
13. От точки к плоскости проведены две наклонные длиной 23 см и 33 см. Вычислить расстояние от этой точки до плоскости, если проекции наклонных относятся как 2:3
14. Расстояние от точки к плоскости треугольника равно 1,1 м, а до каждой из вершин 6,1 м. Вычислить радиус описанной окружности, длину стороны треугольника.
15. От точек А и В, лежащих в перпендикулярных плоскостях, опущены перпендикуляры АК и ВД на прямую пересечения плоскостей. Вычислить длину отрезка АВ, если АК = 3м , ВД = 4 м, КД = 12 м.
16. В прямоугольном параллелепипеде заданы размеры 2 дм, 5дм, 7дм. Вычислите площадь поверхности, длину диагоналей боковых сторон и большей диагонали, длину всех ребер заданного параллелепипеда.
17. Основание пирамиды – прямоугольник со сторонами 6 см и 8 см. Каждое боковое ребро 13 см. Вычислите высоту пирамиды.
18. Расстояние от точки до плоскости треугольника равно 8 м, а до каждой из сторон 10 м. Вычислить радиус вписанной окружности, длину стороны треугольника.
19. Вычисление объма и\или площади поверхности конуса, цилиндра, шара (сферы), куба (и\или элементов по заданным объему, площади)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|