Хелпикс

Главная

Контакты

Случайная статья



Домашнее задание №2 «СЛУЧАЙНЫЕ ПРОЦЕССЫ»



 Домашнее задание №2 «СЛУЧАЙНЫЕ ПРОЦЕССЫ»

Задача 2. Моделирование двумерного винеровского процесса

Алгоритм

Пусть необходимо найти значения двумерного винеровского процесса 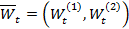 интенсивности  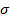в точках вида 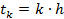, причем .

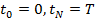1) Полагаем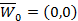

2) Для каждого 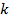 моделируем пару  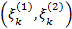независимых нормально распределенных случайных величин с нулевыми математическими ожиданиями и дисперсиями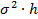

3) Вычисляем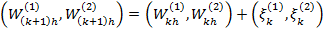

4) Результат – последовательность точек 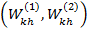. Соединив эти точки для наглядности отрезками прямых, получим смоделированную траекторию.

Задание

1. На интервале 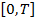 смоделируйте  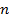траекторий двумерного винеровского процесса интенсивности  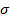с шагом .

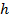2. Выведите на печать 5-7 траекторий (мультимедийность приветствуется)

3.  Для каждой траектории вычислите

1) вариации компонент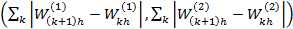

Найдите среднее значение вариации 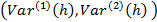 по всем траекториям

2) суммы квадратов приращений компонент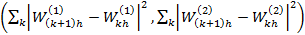

Найдите среднее значение этих сумм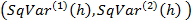

 

4. Уменьшите значение 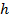 в два раза и вычислите  и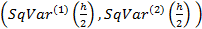

Сравните полученные значения для исходного и уменьшенного шага и объясните результат.

5. Вычислите теоретическую вероятность 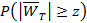 и сравните ее с эмпирической вероятностью достижения указанного уровня  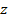 в момент .

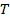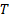
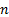
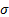
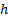
Вар Вар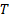
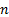
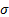
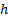
0.4 0.1 0.75 0.04 2.5
0.6 0.05 0.02 3.5
0.3 0.1 1.2 0.01 3.5
0.5 0.08 0.25 0.1 1.5
0.5 0.04 0.75 0.05
0.75 0.02 0.6 0.08
0.01 2.5 0.6 0.04 1.5
0.3 0.1 2.5 0.75 0.02 2.5
0.4 0.05 0.8 0.01 2.5
0.25 0.1 0.2 0.1 1.5
0.4 0.08 3.5 0.5 0.05

Данные

       

 

 

 
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.