Задание 3 № 36016. Задание 4 № 36017. Задание 5 № 36018. Задание 6 № 36019. Задание 7 № 36020. Задание 8 № 36021. Задание 9 № 36022. Задание 10 № 36023. Задание 11 № 36024. Задание 12 № 36025. Задание 13 № 36026. Задание 14 № 36027. Задание 15 № 36028. За

3. Задание 3 № 36016

Даны фрагменты двух таблиц из базы данных. Каждая строка таблицы 2 содержит информацию о ребёнке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке таблицы 1. Определите на основании приведённых данных ID дедушки Аганян Б. Г.

Таблица 1
ID	Фамилия И.О.	Пол
	Дурново И. М.	Ж
	Виеру А. В.	М
	Виеру В. А.	М
	Виеру В. В.	М
	Аганян Т. А.	Ж
	Аганян Б. Г.	Ж
	Аганян Г. Г.	М
	Баурн А. С.	Ж
	Баурн В. А.	М
	Альберт К. Г.	Ж
	Альберт И. К.	М
	Лещенко Н. В.	Ж
	Чивадзе Г. В.	Ж

Таблица 2
ID Родителя	ID Ребенка

Примечание. Дедушка — это отец одного из родителей.

4. Задание 4 № 36017

По каналу связи передаются сообщения, содержащие только четыре буквы: З, А, Р, Я; для передачи используется двоичный код, удовлетворяющий условию Фано. Для букв Я, Р, З используются такие кодовые слова: Я — 0, Р — 101; З — 110.

Укажите кратчайшее кодовое слово для буквы А, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наибольшим числовым значением.

Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.

5. Задание 5 № 36018

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1. Строится двоичная запись числа N.

2. К этой записи дописываются справа ещё два разряда по следующему правилу:

а) складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;

б) над этой записью производятся те же действия — справа дописывается остаток от деления суммы её цифр на 2.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите минимальное число R, которое превышает число 396 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.

6. Задание 6 № 36019

Определите, при каком наибольшем введённом значении переменной s программа выведет число 64. Для Вашего удобства программа представлена на четырёх языках программирования.

Python	Си++
s = int(input()) n = 1 while s < 47: s = s + 4 n = n * 2 print(n)	#include <iostream> using namespace std; int main() { int s, n; cin >> s; n = 1; while (s < 47) { s = s + 4; n = n * 2; } cout << n << endl; return 0; }
Паскаль	Алгоритмический язык
var s, n: integer; begin readln(s); n := 1; while s < 47 do begin s := s + 4; n := n * 2 end; writeln(n) end.	алг нач цел n, s ввод s n := 1 нц пока s < 47 s := s + 4 n := n * 2 кц вывод n кон

7. Задание 7 № 36020

Для хранения произвольного растрового изображения размером 1536 × 2048 пикселей отведено не более 6 Мбайт памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?

8. Задание 8 № 36021

Вася составляет 6-буквенные слова, в которых могут быть использованы только буквы В, И, Ш, Н, Я, причём буква В используется не более одного раза. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Слово не должно начинаться с буквы Ш и оканчиваться гласными буквами. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася?

9. Задание 9 № 36022

Откройте файл электронной таблицы, содержащей вещественные числа — результаты ежечасного измерения температуры воздуха в течение трёх месяцев. Найдите разность между максимальной температурой воздуха с 1 апреля по 31 мая с 9:00 до 12:00 включительно и средним значением температуры воздуха в эти часы в апреле и мае, используя данные, представленные в таблице.

В ответе запишите только целую часть получившегося числа.

Задание 9

10. Задание 10 № 36023

Определите, сколько раз в тексте произведения А. С. Грибоедова «Горе от ума», не считая сносок, встречается слово «батюшка» или «Батюшка». Другие формы слова «батюшка», такие как «батюшке», «батюшки» и т. д., учитывать не следует. В ответе укажите только число.

Задание 10

11. Задание 11 № 36024

При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 32 символов и содержащий только десятичные цифры и символы из 240-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование идентификаторов, все символы кодируют одинаковым и минимально возможным количеством бит.

Определите объём памяти (в Кбайт), необходимый для хранения 3200 идентификаторов. В ответе запишите только целое число — количество Кбайт.

12. Задание 12 № 36025

Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.

А) заменить (v, w).

Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды

заменить (111, 27)

преобразует строку 05111150 в строку 0527150.

Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.

Б) нашлось (v).

Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка

исполнителя при этом не изменяется.

Цикл

ПОКА условие

последовательность команд

КОНЕЦ ПОКА

выполняется, пока условие истинно.

В конструкции

ЕСЛИ условие

ТО команда1

КОНЕЦ ЕСЛИ

выполняется команда1 (если условие истинно).

В конструкции

ЕСЛИ условие

ТО команда1

ИНАЧЕ команда2

КОНЕЦ ЕСЛИ

выполняется команда1 (если условие истинно) или команда2 (если условие ложно).

Дана программа для редактора:

НАЧАЛО

ПОКА нашлось (1111) ИЛИ нашлось (88888)

ЕСЛИ нашлось (1111)

ТО заменить (1111, 888)

ИНАЧЕ заменить (88888, 888)

КОНЕЦ ЕСЛИ

КОНЕЦ ПОКА

КОНЕЦ

Какая строка получится в результате применения приведённой выше программы к строке, состоящей из 81 идущей подряд цифры 1? В ответе запишите полученную строку.

13. Задание 13 № 36026

На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, проходящих через город Ж и не проходящих через город К?

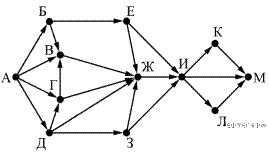
14. Задание 14 № 36027

Значение арифметического выражения

7 · 512¹²⁰ − 6 · 64¹⁰⁰ + 8²¹⁰ − 255

записали в системе счисления с основанием 8. Сколько цифр 0 содержится в этой записи?

15. Задание 15 № 36028

На числовой прямой даны два отрезка: P = [17, 54] и Q = [37, 83]. Какова наименьшая возможная длина интервала A, что формула

(x ∈ P) → (((x ∈ Q) ∧ (x ∈ A)) → (x ∈ P))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

16. Задание 16 № 36029

Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:

F(1) = 1;

F(n) = n + F(n − 1), если n чётно;

F(n) = 2 · F(n − 2), если n > 1 и при этом нечётно.

Чему равно значение функции F(24)?

17. Задание 17 № 36030

Рассматривается множество целых чисел, принадлежащих числовому отрезку [16 015; 48 989], которые делятся на 7 или 11 и не делятся на 9, 12, 13. Найдите количество таких чисел и минимальное из них. В ответе запишите два целых числа: сначала количество, затем минимальное число.

Для выполнения этого задания можно написать программу или воспользоваться редактором электронных таблиц.

18. Задание 18 № 36031

Квадрат разлинован на N × N клеток (1 < N < 26). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку; по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата указана плата за посещение в размере от 1 до 100. Посетив клетку, Робот платит за её посещение; это также относится к начальной и конечной клеткам маршрута Робота.

Определите минимальную и максимальную денежные суммы, которые заплатит Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа: сначала минимальную сумму, затем максимальную, без разделительных знаков. Исходные данные представляют собой электронную таблицу размером N × N, каждая ячейка которой соответствует клетке квадрата.

Исходные данные записаны в электронной таблице.

Задание 18

Пример входных данных (для таблицы размером 4 × 4):

Для указанных входных данных ответом должна быть пара чисел: 22 и 41.

19. Задание 19 № 36032

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 5 камней, а в другой 9 камней; такую позицию мы будем обозначать (5, 9). За один ход из позиции (5, 9) можно получить любую из четырёх позиций: (6, 9), (10, 9), (5, 10), (5, 18).

Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 107. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 107 или больше камней.

В начальный момент в первой куче было 13 камней, во второй куче — S камней; 1 ≤ S ≤ 93.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т. е. не являющиеся выигрышными независимо от игры противника.

Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна

20. Задание 20 № 36033

В начальный момент в первой куче было 13 камней, во второй куче — S камней; 1 ≤ S ≤ 93.

Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:

— Петя не может выиграть за один ход;

— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.

21. Задание 21 № 36034

В начальный момент в первой куче было 13 камней, во второй куче — S камней; 1 ≤ S ≤ 93.

Найдите минимальное значение S, при котором одновременно выполняются два условия:

— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

22. Задание 22 № 36035

Ниже на четырёх языках программирования записан алгоритм. Получив на вход число x, этот алгоритм печатает два числа: L и M. Укажите наименьшее число x, при вводе которого алгоритм печатает сначала 5, а потом 8.

C++	Python
#include <iostream> using namespace std; int main() { int x, L, M; cin >> x; L = 0; M = 0; while (x > 0){ M = M + 1; if(x % 2 != 0){ L = L + 1; } x = x / 2; } cout << L << endl << M << endl; return 0; }	x = int(input()) L = 0 M = 0 while x > 0: M = M + 1 if x % 2 != 0: L = L + 1 x = x // 2 print(L) print(M)
Паскаль	Алгоритмический язык
var x, L, M: integer; begin readln(x); L := 0; M := 0; while x > 0 do begin M := M + 1; if x mod 2 <> 0 then L := L + 1; x := x div 2; end; writeln(L); writeln(M); end.	алг нач цел x, L, M ввод x L := 0 M := 0 нц пока x > 0 M := M + 1 если mod(x, 2) <> 0 то L := L + 1 все x := div(x, 2) кц вывод L, нс, M кон

23. Задание 23 № 36036

Исполнитель Минус преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:

1. Вычесть 2

⇐ Предыдущая 123 4 Следующая ⇒