
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение заданий ЕГЭ (профильный уровень)
Решение заданий ЕГЭ (профильный уровень)
Вариант №24563379
Задание 1. На корабле плывёт 500 пассажиров и 15 членов команды. Сколько шлюпок потребуется, чтобы перевезти всех людей с корабля на берег, если в одну шлюпку помещается 80 человек.
Решение:
1) Находим общее количество людей на корабле 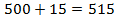 .
.
2) Теперь находим сколько шлюпок понадобится 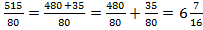 .
.
Ответ: 7
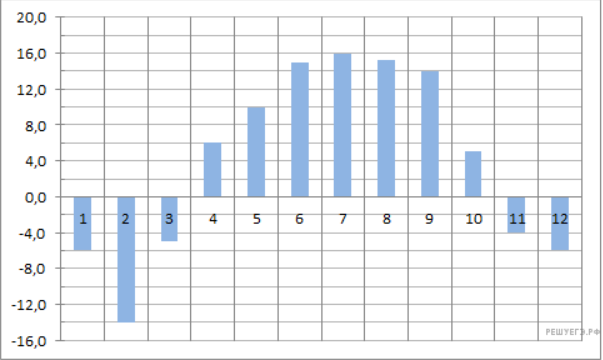
Задание 2.На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в период с января по апрель 1994 года. Ответ дайте в градусах Цельсия.
Решение:
Из диаграммы видно, что наибольшая среднемесячная температура с 1 по 4 месяц составляла 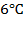 .
.
Ответ: 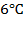
Задание 3. Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1×1 см. Ответ дайте в квадратных сантиметрах.
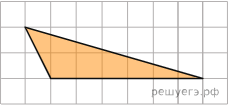
Решение:
Проводим высоту, площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию 
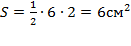 .
.
Ответ: 6
Задание 4. В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по теме "Неравенства". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по теме "Неравенства".
Решение:
1) Найдем сколько билетов без темы "Неравенства" Þ 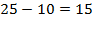 .
.
2) Вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по теме "Неравенства", находится по формуле 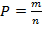 ,
,
тогда 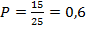 .
.
Ответ: 0,6
Задание 5.Решите уравнение 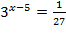
Решение:
Приведем уравнение к одному основание степени 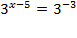 Þ
Þ 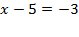 Þ
Þ 
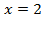 .
.
Ответ: 2
Задание 6. В четырёхугольник ABCD вписана окружность, AB=10, BC=8, CD=16. Найдите длину стороны AD.
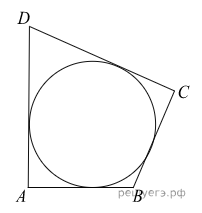
Решение:
1) По свойству: Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин его противоположных сторон равны, а значит 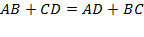

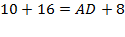 .
.
2) Находим сторону AD следующим образом, 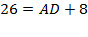 Þ
Þ
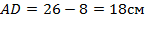 .
.
Ответ: 18
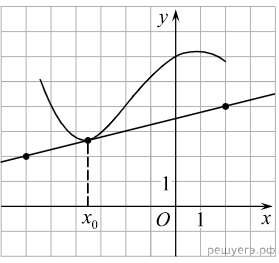
Задание 7. На рисунке изображён график функции 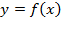 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой 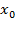 . Найдите значение производной функции
. Найдите значение производной функции 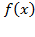 в точке
в точке 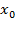 .
.
Решение:
1) Построим треугольник с вершинами в точках A (2; 4), B (−6; 2), C (2; 2). Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс.
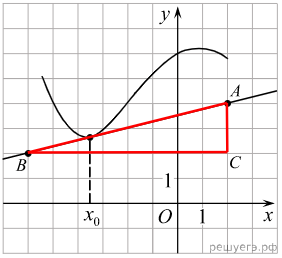
2) Угол наклона касательной к оси абсцисс будет равен углу ABC. Поэтому 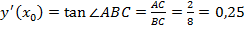 .
.
Ответ: 0,25
Задание 8. Во сколько раз изменится объём конуса, если его высота уменьшится в 12 раз, а радиус основания не изменился.
Решение:
1) Рассмотри формулу нахождения объема конуса 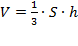 , где S – площадь основания, а h – высота конуса.
, где S – площадь основания, а h – высота конуса.
2) Исходя из формулы, мы видим, что если высота уменьшится в 12 раз, то и сам объем тоже уменьшится в 12 раз.
Ответ: 12
Задание 9. Найдите значение выражения 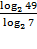
Решение:
1) Воспользуемся свойством логарифма: Переход к новому основанию 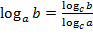 Þ
Þ 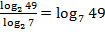 .
.
2) Теперь вычислим логарифм по определению: Логарифм по основанию a от аргумента x - это степень, в которую надо возвести число a, чтобы получить число x, тогда 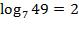 .
.
Ответ: 2
Задание 10. При сближении источника и приёмника звуковых сигналов движущихся в некоторой среде по прямой навстречу друг другу частота звукового сигнала, регистрируемого приeмником, не совпадает с частотой исходного сигнала 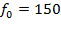 Гц и определяется следующим выражением:
Гц и определяется следующим выражением: 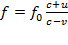 (Гц), где c – скорость распространения сигнала в среде (в м/с), а u=10 м/с и v=15 м/с – скорости приeмника и источника относительно среды соответственно. При какой максимальной скорости c (в м/с) распространения сигнала в среде частота сигнала в приeмнике f будет не менее 160 Гц?
(Гц), где c – скорость распространения сигнала в среде (в м/с), а u=10 м/с и v=15 м/с – скорости приeмника и источника относительно среды соответственно. При какой максимальной скорости c (в м/с) распространения сигнала в среде частота сигнала в приeмнике f будет не менее 160 Гц?
Решение:
1) Запишем выражения частоты в виде неравенства 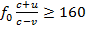 .
.
2) Подставляем все известные нам значения 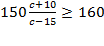 Þ
Þ 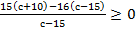

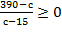 Þ
Þ 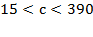 м/c.
м/c.
Ответ: 390
Задание 11. Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 77 км. На следующий день он отправился обратно в A со скоростью на 4 км/ч больше прежней. По дороге он сделал остановку на 4 часа. B результате велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из B в A. Ответ дайте в км/ч.
Решение:
1) Введем обозначения, Пусть v км/ч – скорость велосипедиста на пути из B в A, тогда скорость велосипедиста на пути из A в B равна 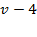 км/ч.
км/ч.
2) Сделав на обратном пути остановку на 4 часа, велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B, отсюда имеем:
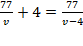 Þ
Þ 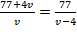 Þ
Þ
3) Решаем пропорцию: 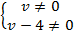
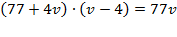 Þ
Þ 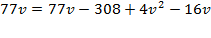 Þ
Þ
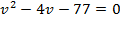 Þ
Þ
4) Решаем квадратное уравнение: 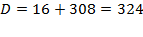 Þ
Þ 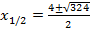
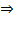
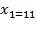 Þ
Þ 
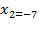 Þ Скорость не может выражаться отрицательным значением, а тогда скорость велосипедиста составляет 11км/ч.
Þ Скорость не может выражаться отрицательным значением, а тогда скорость велосипедиста составляет 11км/ч.
Ответ: 11
Задание 12. Найдите точку максимума функции 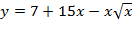 .
.
Решение:
1) Найдем производную заданной функции:
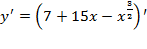 Þ
Þ 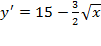 .
.
2) Найдем нули производной: 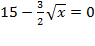 Þ
Þ 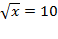 Þ
Þ 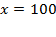 .
.
3) Определим знаки производной функции и изобразим на рисунке поведение функции:
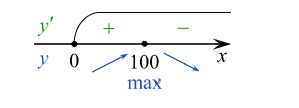
Искомая точка максимума 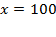 .
.
Ответ: 100
Задание 13. (а) Решите уравнение 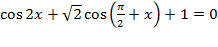 .
.
(б) Найдите все корни этого уравнения, принадлежащие отрезку 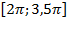 .
.
Решение:
1) а. Воспользуемся формулой косинуса двойного угла: 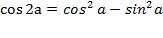 , а также формулой приведения:
, а также формулой приведения:
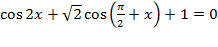
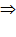
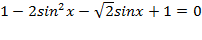 Þ
Þ
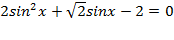
2) Пусть 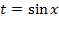 , тогда:
, тогда:
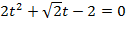 Þ
Þ 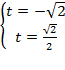
3) Ввернемся к исходной переменной:
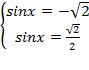 Þ
Þ 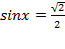 Þ
Þ 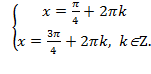
1) б. С помощью числовой окружности отберем корни уравнения, принадлежащие отрезку 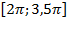 .
.
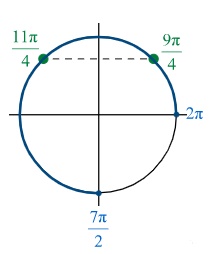
2) Получаем числа: 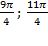 .
.
Ответ: а) 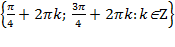 ; б)
; б) 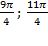 .
.
Задание 14. В правильной треугольной пирамиде SABC точка P — делит сторону AB в отношении 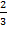 , считая от вершины A, точка K — делит сторону BC в отношении
, считая от вершины A, точка K — делит сторону BC в отношении 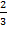 , считая от вершины C. Через точки P и K параллельно SB проведена плоскость w.
, считая от вершины C. Через точки P и K параллельно SB проведена плоскость w.
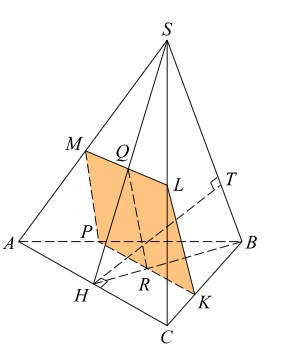
а) Докажите, что сечение пирамиды плоскостью w является прямоугольником.
б) Найдите расстояние от точки S до плоскости w, если известно, что SC=5, AC=6.
Решение:
1) а. Построим сечение пирамиды плоскостью w. Заметим, что BP=BK, поэтому треугольники PBK и ABC подобны, а тогда PK || AC. Поскольку плоскость w проходит через прямую PK, параллельную плоскости ASC, w пересекает ASC по прямой, параллельной PK. Пусть эта прямая пересекает SA и SC в точках M и L соответственно. Тогда прямые PK, AC и LM параллельны.
2) По условию, w||SB, поэтому прямые MP и LK параллельны SB, а значит, параллельны между собой. Тогда в четырёхугольнике LMKP противоположные стороны попарно параллельны. Следовательно, сечение — параллелограмм.
3) Скрещивающиеся рёбра правильной пирамиды взаимно перпендикулярны, поэтому перпендикулярны соответственно параллельные им прямые LM и LK. Тем самым, стороны сечения перпендикулярны, следовательно, сечение — прямоугольник. Это и требовалось доказать.
1) б. Пусть H — середина AC. Проведём SH и BH и пусть плоскость SHB пересекает w по прямой QR. Тогда QR || SB, а расстояние от точки S до плоскости w равно d(SB, QR) — расстоянию между параллельными прямыми SB и QR. Найдем его.
2) В треугольнике SHB длина SB=5, BH= 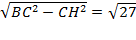 , SH=
, SH= 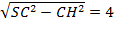 . Проведём высоту треугольника HT и найдем её. Пусть BT = x, тогда ST =
. Проведём высоту треугольника HT и найдем её. Пусть BT = x, тогда ST = 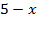 , тогда, применяя теорему Пифагора из треугольников BHT и SHT получаем:
, тогда, применяя теорему Пифагора из треугольников BHT и SHT получаем:
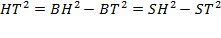 .
.
3) Подставляем наши значения: 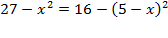 Þ
Þ 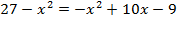 Þ
Þ 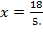
4) Тогда мы можем найти HT:
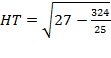 Þ
Þ 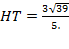
5) По условию 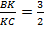 , поэтому
, поэтому 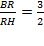 , а тогда поскольку сечение делит высоту HT в том же отношении, считая от точки T, тогда:
, а тогда поскольку сечение делит высоту HT в том же отношении, считая от точки T, тогда:
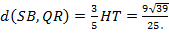
Ответ: б) 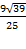
Задание 15. Решите неравенство 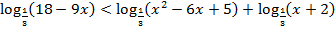 .
.
Решение:
1) Если основание логарифма больше нуля и меньше единицы (0<p(x)<1), то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства меняется на противоположный, тогда преобразуем неравенство:
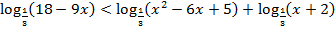 Þ
Þ 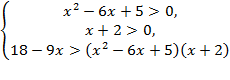 Þ Решаем полученную систему неравенств
Þ Решаем полученную систему неравенств
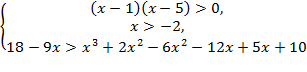 Þ
Þ 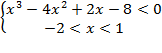
2) Рассмотрим первое неравенство системы:
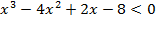 Þ
Þ 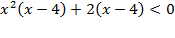 Þ
Þ 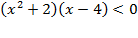 .
.
3) Первый множитель больше нуля, следовательно, знак выражения определяется вторым множителем и решение неравенства: 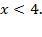 Учитывая второе неравенство, получаем решение исходного неравенства:
Учитывая второе неравенство, получаем решение исходного неравенства: 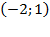 .
.
Ответ: 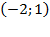
Задача 16. Около 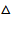 ABC описана окружность. Прямая BO, где O — центр вписанной окружности, вторично пересекает описанную окружность в точке P.
ABC описана окружность. Прямая BO, где O — центр вписанной окружности, вторично пересекает описанную окружность в точке P.
а) Докажите, что OP=AP.
б) Найдите расстояние от точки P до прямой AC, если 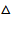 ABC=
ABC= 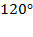 , а радиус описанной окружности равен 18.
, а радиус описанной окружности равен 18.
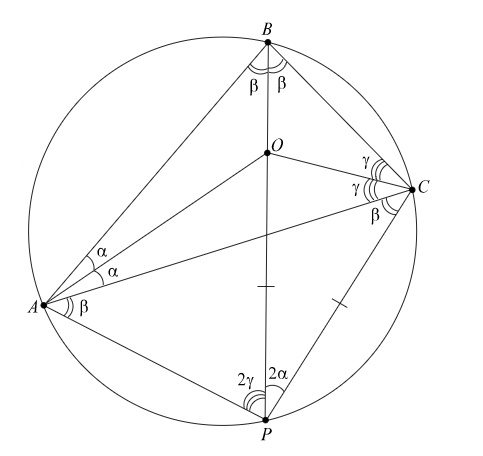
Решение:
1) а. Обозначим углы треугольника ABC: 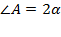 ,
, 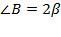 ,
, 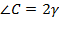 .
.
2) Заметим, что 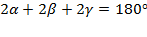 ,
, 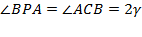 (как вписанные углы, опирающиеся на одну дугу). По аналогии
(как вписанные углы, опирающиеся на одну дугу). По аналогии 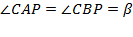 .
.
3) Находим 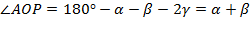 , но мы знаем, что
, но мы знаем, что 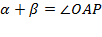 , тогда треугольник AOP – равнобедренный Þ AP=OP.
, тогда треугольник AOP – равнобедренный Þ AP=OP.
1) б. Сумма противоположных углов вписанного четырехугольника равна 180  Þ
Þ 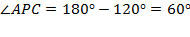 ,
, 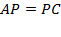 (как хорды, стягивающие равные дуги). Þ треугольник APC – равносторонний.
(как хорды, стягивающие равные дуги). Þ треугольник APC – равносторонний.
2) Искомое расстояние d равно его высоте: d= 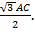
3) По теореме синусов: стороны треугольника пропорциональны синусам противолежащих углов Þ 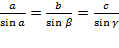 Þ
Þ 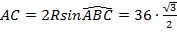 Þ
Þ 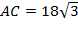 Þ
Þ 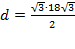 Þ
Þ 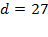 (расстояние от точки P до прямой АС).
(расстояние от точки P до прямой АС).
Ответ: 27
Задание 17. В июле планируется взять кредит в банке на сумму 6 млн рублей на срок 15 лет. Условия его возврата таковы:
— каждый январь долг возрастает на x% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
Найдите x, если известно, что наибольший платёж по кредиту составит не более 1,9 млн рублей, а наименьший — не менее 0,5 млн рублей.
Решение:
1) Долг перед банком по состоянию на июль должен уменьшаться до нуля равномерно, ежегодно уменьшаясь на одну пятнадцатую. Поэтому первый платеж составит одну пятнадцатую от 6 миллионов (возврат первой части тела долга) и процент за их использование. Последний платеж также составит одну пятнадцатую от 6 миллионов (возврат последней части тела долга) и процент за использование этой суммы в течение последнего года:
Первая выплата (в млн.): 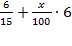
Вторая выплата (в млн.): 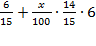
Третья выплата (в млн.): 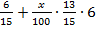
Пятнадцатая выплата (в млн.): 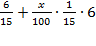
Все выплаты (в млн.): 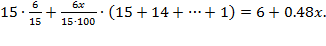
2) Поскольку наибольший годовой платеж ( 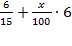 ) по кредиту составит не более 1,9 млн. рублей, а наименьший (
) по кредиту составит не более 1,9 млн. рублей, а наименьший ( 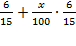 ) – не менее 0,5 млн. рублей, получаем два линейных неравенства:
) – не менее 0,5 млн. рублей, получаем два линейных неравенства:
а) 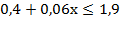 Þ
Þ 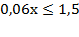 Þ
Þ 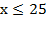 .
.
б) 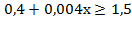 Þ
Þ 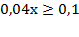 Þ
Þ 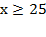 .
. 
Из полученного х=25.
Ответ: 25
Задание 18. При каких значениях параметра a уравнение 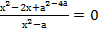 имеет ровно 2 различных решения.
имеет ровно 2 различных решения.
Решение:
1) 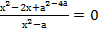
Уравнение равносильно системе
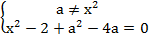
Второе уравнение преобразуем выделением полного квадрата, тогда получим:
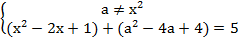 Þ
Þ
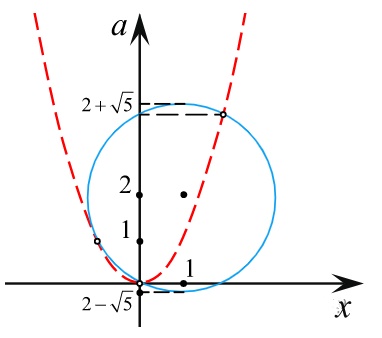
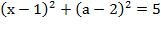 (уравнение окружности с координатами (х ; а). Þ
(уравнение окружности с координатами (х ; а). Þ
1.1 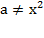 – парабола Þ (0;0) – вершина.
– парабола Þ (0;0) – вершина.
1.2 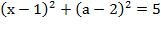 – окружность Þ (1;2) – центр,
– окружность Þ (1;2) – центр, 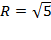 .
.
2) Найдем точки пересечения окружности и параболы:
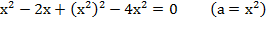 Þ
Þ
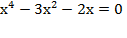 Þ
Þ
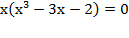 Þ
Þ
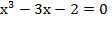 Þ х=0, а=0
Þ х=0, а=0
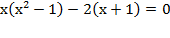 Þ
Þ
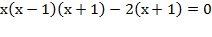 Þ
Þ
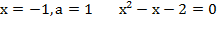 Þ
Þ
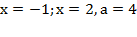 .
.
3) 2 решения: 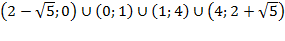 .
.
Ответ: 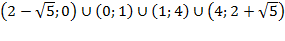 .
.
Задание 19. Последовательность натуральных чисел 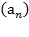 состоит из 400 членов. Каждый член последовательности, начиная со второго, либо вдвое больше предыдущего, либо на 98 меньше предыдущего.
состоит из 400 членов. Каждый член последовательности, начиная со второго, либо вдвое больше предыдущего, либо на 98 меньше предыдущего.
а) Может ли последовательность 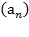 содержать ровно 5 различных чисел?
содержать ровно 5 различных чисел?
б) Чему может равняться 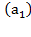 , если
, если 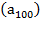 =75?
=75?
в) Какое наименьшее значение может принимать наибольший член последовательности 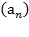 ?
?
Решение:
A) Пусть a — первое число. Постараемся найти цепочку вида:
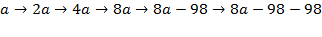
Для зацикливания требуется, чтобы 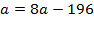 . Это уравнение имеет натуральное решение:
. Это уравнение имеет натуральное решение: 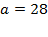 . Действительно, имеем цепочку, состоящую из пяти чисел:
. Действительно, имеем цепочку, состоящую из пяти чисел:
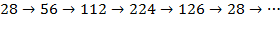
Б) По условию или 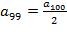 , или
, или 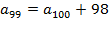 . Но
. Но 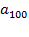 — нечетное число, поэтому есть ровно одна возможность:
— нечетное число, поэтому есть ровно одна возможность: 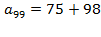 — снова нечетное число, поэтому для
— снова нечетное число, поэтому для 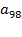 снова ровно одна возможность. Так всякий раз будут получаться нечетные числа, поскольку сумма нечетного и четного чисел является нечетным числом. Рассуждая аналогично, получаем:
снова ровно одна возможность. Так всякий раз будут получаться нечетные числа, поскольку сумма нечетного и четного чисел является нечетным числом. Рассуждая аналогично, получаем: 
В) 1. Заметим, что цепочка
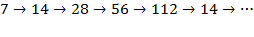
удовлетворяет условиям.
2. Докажем, что наибольший член последовательности не может быть меньше 112. Пусть a — наибольший член последовательности (начиная с момента, когда впервые произошло умножение на 2; заметим, что в нашем случае 98 не может вычитаться дважды подряд). Тогда предыдущее число - это 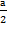 . Следовательно, a — четное.
. Следовательно, a — четное.
3. Значение 98 и меньше а быть не может, так как это бы означало, что в нашей цепочке, начиная с первого умножения на 2, ни разу не вычиталось 98. Следовательно, с этого момента были только умножения на 2. Но тогда, очевидно, нашелся бы член последовательности, который больше 112. Поэтому достаточно рассмотреть случаи, когда a равно 110, 108, 106, 104, 102, 100.
4. Переберем эти значения. Рассмотрим момент, когда a появился впервые (очевидно, номер этого члена последовательности заведомо не превзойдет, например, 10).
* В случае значений a, равных 100, 102, 106, после вычитания 98 (на следующем шаге), мы попадем в элемент цепочки:
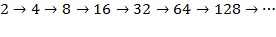
и найдется член, который превзойдет 112 (и будет равен по крайней мере 128).
* Значения a, равные 104 и 110, приведут нас в элемент цепочки
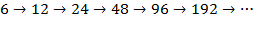
* Значение a=108 приведет нас к цепочке
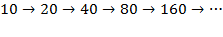
и вновь найдется член, который превзойдет 112 (и будет равен, по крайней мере, 160).
Ответ: а) да, б) 9777, в)112
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|