
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
МАТЕМАТИКА. КУРС 1 СЕМЕСТР. Выполните задание. В таблице ответов рядом с номером задания (1 – 20) запишите номер выбранного Вами правильного ответа.
МАТЕМАТИКА
1 КУРС 1 СЕМЕСТР
Для оформления ответов необходимо заполнить следующую таблицу.
ФИО студента, шифр группы.
| Номер задания | ||||||||||||||||||||
| Номер ответа |
Результат выслать 15.01.2021 до 12.00 на почту valmg@inbox.ru или на 80951645365 (Viber)
К каждому заданию теста даны пять ответов, из которых только один является верным.
Выполните задание. В таблице ответов рядом с номером задания (1 – 20) запишите номер выбранного Вами правильного ответа.
| СОДЕРЖАНИЕ ЗАДАНИЯ | ВАРИАНТЫ ОТВЕТА |
| 1. Даны точки A(0, –2, 3); В(2, 4, –1). Найти расстояние между ними. | 1) 7; 2) 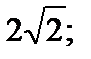 3) 12; 4) 3) 12; 4) 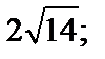 5) 8. 5) 8.
|
| 2. Перемножить числа 2 – 3i; –1 + 2i. | 1) –2 – 6i; 2) 4 – i; 3) 1 – 5i; 4) 8 – i; 5) 4 + 7i. |
3. Вычислить А – 2В, где  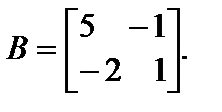 В ответе указать сумму всех элементов полученной матрицы. В ответе указать сумму всех элементов полученной матрицы.
| 1) 15; 2) –5; 3) 17; 4) –4; 5) 5. |
4. Выяснить, при каком значении a векторы ортогональны: 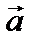 = (–2, 3, a); = (–2, 3, a); 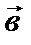 = (4, –6, –8). = (4, –6, –8).
| 1)- 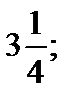 2) –2; 3) 0; 4) –4; 5) 1. 2) –2; 3) 0; 4) –4; 5) 1.
|
5. Вычислить 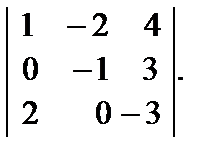
| 1) 1; 2) 7; 3) –1; 4) –7; 5) 5. |
6. Определить тип линии 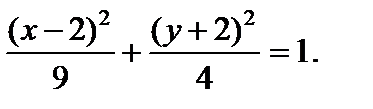
| 1) парабола; 2) гипербола; 3) окружность; 4) эллипс; 5) пересекающиеся прямые. |
7. Вычислить 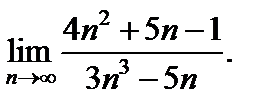
| 1) 0; 2) 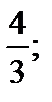 3) –1; 4) ¥; 5) 3) –1; 4) ¥; 5) 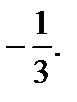
|
8. Вычислить 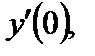 если если 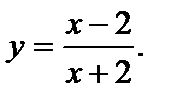
| 1) 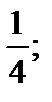 2) 1; 3) 0; 4) 4; 5) 2) 1; 3) 0; 4) 4; 5) 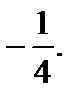
|
9. Определить точку минимума функции 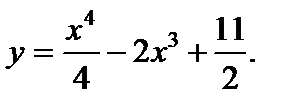
| 1) 0; 2) 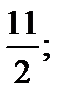 3) 1; 4) 3) 1; 4) 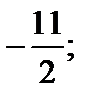 5) 6. 5) 6.
|
10. Вычислить 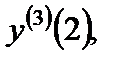 если если 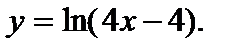
| 1) ln4; 2) 2; 3) 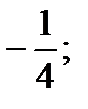 4) –6; 5) 0. 4) –6; 5) 0.
|
11. Вычислить скалярное произведение векторов 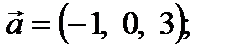 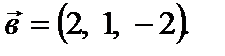
| 1) 6; 2) 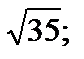 3) 3) 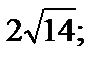 4) 3; 5) –8. 4) 3; 5) –8.
|
12. Вычислить 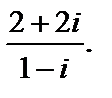 Полученное комплексное число записать в алгебраической форме. Полученное комплексное число записать в алгебраической форме.
| 1) –2; 2) 1 + 2i; 3) –2i; 4) 2i; 5) 2 – i. |
13. Решить матричное уравнение 2А + X = В, где 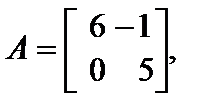 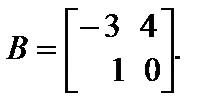 В ответе указать сумму всех элементов полученной матрицы. В ответе указать сумму всех элементов полученной матрицы.
| 1) 2; 2) 15; 3) 8; 4) –18; 5) –20. |
14. Выяснить, при каком значении a векторы коллинеарны: 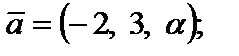 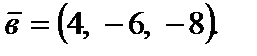
| 1) 3; 2) –2; 3) 0; 4) 1; 5) 4. |
15. Вычислить 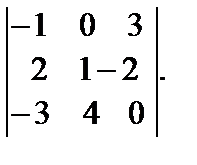
| 1) 13; 2) 25; 3) 33; 4) 8; 5) 24. |
16. Определить координаты центра окружности 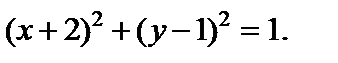
| 1) (2, –1); 2) (–4, 0); 3)(–2, 1); 4) (–4, 2); 5) (2, –4). |
17. Вычислить 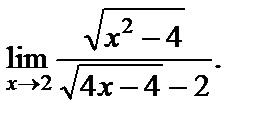
| 1) ¥; 2) 1; 3) 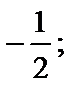 4) 2; 5) 0. 4) 2; 5) 0.
|
18. Вычислить 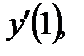 если если 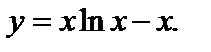
| 1) 1; 2)–1; 3) 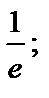 4) е; 5) 0. 4) е; 5) 0.
|
19. Определить абсциссу точки (для x > 0), в которой касательная к графику функции  параллельна оси Ox. параллельна оси Ox.
| 1) 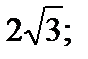 2) 0; 3) 2; 4) 6; 5) 12. 2) 0; 3) 2; 4) 6; 5) 12.
|
20. Вычислить 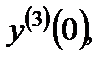 если если 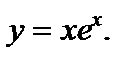
| 1) 4; 2) 3; 3) 1; 4) 3e; 5) 0. |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|