Целые уравнения.. Уравнение с одной переменной называют целым уравнением, если обе его части являются целыми выражениями.. Уравнения первой и второй степени вы уже знаете как решать. Для квадратных уравнений существуют формулы корней.. Многие уравнения 3-

Целые уравнения.

1. Решите уравнение:

а) х – 2 = 3; б) 7х = 11; в) 1,5х = 0;

г) х² – 9 = 0; д) 3х² – 75 = 0; е) 0,7х² = 0;

ж) 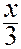= 12; з) 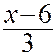= 12.

2. Что значит решить уравнение?

3. Какие выражения называют целыми?

Уравнение с одной переменной называют целым уравнением, если обе его части являются целыми выражениями.

Посмотрите примеры уравнений на странице 156 учебника. Первая пара уравнений относится к целым уравнениям, следующая пара – к дробным уравнениям.

Любое целое уравнение можно преобразовать в равносильное ему уравнение вида р(х) = 0, где р(х) – многочлен стандартного вида.

Например, уравнение х²(х – 1) + 4 = х(8 – х²). Приведём его к стандартному виду.

2х³ – х² – 8х + 4 = 0 – уравнение третьей степени.

х⁴ + 2х² – 15 = 0 – уравнение четвёртой степени.

х⁵ + 4х³ = 0 – уравнение пятой степени.

Уравнения первой и второй степени вы уже знаете как решать. Для квадратных уравнений существуют формулы корней.

Многие уравнения 3-й степени и выше трудны в решении. Некоторые даже не имеют действительных корней.

Рассмотрим приёмы решения некоторых «хороших» уравнений 3-й и 4-й степеней.

Один из методов – разложение многочлена на множители.

Решим уравнение: 2х³ – х² – 8х + 4 = 0

В классе № 380 (г,д,е), 383 (в,г), 384 (б,д), 386*(а)

Домашнее задание:

п. 3.2 (до примера 2), № 380 (а-в), 383 (а,б), 384 (а,г), 386*(б)